Kết quả tìm kiếm cho: ty so

Đề: Xác định $m$ để các hàm số sau đấy xác định với mọi $x>0$a) $y=\sqrt{x-m}+\sqrt{2x-m-1}$ b) $y=\sqrt{2x-3m+4}+\frac{x-m}{x+m-1}$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tập xác định của hàm số

Đề bài: Xác định $m$ để các hàm số sau đấy xác định với mọi $x>0$a) $y=\sqrt{x-m}+\sqrt{2x-m-1}$ b) $y=\sqrt{2x-3m+4}+\frac{x-m}{x+m-1}$ Lời giải Giảia) Hàm số $y$ xác định $\Leftrightarrow \begin{cases}x-m \geq 0 \\ 2x-m-1 \geq 0 \end{cases} \Leftrightarrow \begin{cases}x \geq m (1) \\ x \geq \frac{m+1}{2} (2) \end{cases}$Do đó … [Đọc thêm...] vềĐề: Xác định $m$ để các hàm số sau đấy xác định với mọi $x>0$a) $y=\sqrt{x-m}+\sqrt{2x-m-1}$ b) $y=\sqrt{2x-3m+4}+\frac{x-m}{x+m-1}$

Đề: a) Tìm tập giá trị của các hàm số $y=x^{2}$b) Với giá trị nào của $x$ thì hàm số $y=0$$y=2x-6; y=x^{2}-25$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Hàm số bậc hai

Đề bài: a) Tìm tập giá trị của các hàm số $y=x^{2}$b) Với giá trị nào của $x$ thì hàm số $y=0$$y=2x-6; y=x^{2}-25$ Lời giải a) Hàm số $y=x^{2}$ xác định với mọi giá trị của $x$ ( nghĩa là $D=R$) và tập giá trị của hàm số là $[0;+\infty)$b) $y=2x-6, y=0$ thì $2x-6=0\Leftrightarrow x=3$$y=x^{2}-25, y=0$ thì $x^{2}-25=0\Leftrightarrow x=\pm5$ … [Đọc thêm...] vềĐề: a) Tìm tập giá trị của các hàm số $y=x^{2}$b) Với giá trị nào của $x$ thì hàm số $y=0$$y=2x-6; y=x^{2}-25$

Đề: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 – \left| x \right|}}$$ a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$ b)$ Tìm $g_0f$ và $f_0g.$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tính chất của hàm số

Đề bài: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 - \left| x \right|}}$$ a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$ b)$ Tìm $g_0f$ và $f_0g.$ Lời giải $a)$ $f(x) = \frac{x}{{1 + \left| x \right|}}$ có miền xác định : $D = R$ $f( - x) = - \frac{x}{{1 + \left| x \right|}} = -f(x) \Rightarrow … [Đọc thêm...] vềĐề: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 – \left| x \right|}}$$ a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$ b)$ Tìm $g_0f$ và $f_0g.$

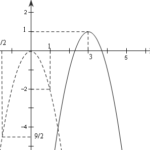
Đề: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2} nếu x\leq -\frac{1}{2} \\ -2x^2+x+3, nếu x>-\frac{1}{2} \end{cases}$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2} nếu x\leq -\frac{1}{2} \\ -2x^2+x+3, nếu x>-\frac{1}{2} \end{cases}$ Lời giải Giải* Xét hàm số bậc nhất $f_1(X)=-x+\frac{3}{2}$ trên khoảng $D_1=(-\infty; -\frac{1}{2}]$Đó là hàm số bậc nhất có $a=-1Tại $x=-\frac{1}{2}, f(-\frac{1}{2})=2$. Tại $x=\frac{3}{2}, f(\frac{3}{2})=0$Đồ thị là đường … [Đọc thêm...] vềĐề: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2} nếu x\leq -\frac{1}{2} \\ -2x^2+x+3, nếu x>-\frac{1}{2} \end{cases}$

Đề: Vẽ đồ thị của hàm số $y=-2x^2+12x-17.$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Vẽ đồ thị của hàm số $y=-2x^2+12x-17.$ Lời giải Ta biến đổi:$y=-2x^2+12x-17=-2(x-3)^2+1.$Từ đó, đồ thị của hàm số $y=-2x^2+12x-17$ được suy từ đồ thị của hàm số $y=-2x^2$ như hình vẽ.Bây giờ sau khi biết rằng đồ thị $(P)$ của hàm số $y=ax^2+bx+c$ là một parabol như trên, để vẽ nó ta thực hiện như sau:- Xác định đỉnh của $(P)$.- Xác định trục đối xứng và hướng bề … [Đọc thêm...] vềĐề: Vẽ đồ thị của hàm số $y=-2x^2+12x-17.$

Đề: Cho hàm số : $y= – x^{4}- x^{2}+6$a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số : $y= - x^{4}- x^{2}+6$a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$ Lời giải a) • Tập xác định : $D=R$• Sự biến thiên : $y’=-4x^{3}-2x=-2x \left( 2 x^{2} +1 \right) =0$$\Leftrightarrow x=0 \Rightarrow y=6$Bảng … [Đọc thêm...] vềĐề: Cho hàm số : $y= – x^{4}- x^{2}+6$a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$

Đề: a) Cho hàm số phân thức dạng $ y=\frac{u}{v}; u, v $ là hàm số của $x$ và có đạo hàm, $v(x)\neq 0$. Chứng minh rằng nếu $y'(x_0)=0$ thì $y(x_0)=\frac{u'(x_0)}{v'(x_0)} $ . b) Cho hàm số $y=\frac{x^2+x-1}{x-1} $. Xác định tọa độ các điểm mà tiếp tuyến tại đó song song với trục hoành.

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tiếp tuyến của đồ thị

Đề bài: a) Cho hàm số phân thức dạng $ y=\frac{u}{v}; u, v $ là hàm số của $x$ và có đạo hàm, $v(x)\neq 0$. Chứng minh rằng nếu $y'(x_0)=0$ thì $y(x_0)=\frac{u'(x_0)}{v'(x_0)} $ . b) Cho hàm số $y=\frac{x^2+x-1}{x-1} $. Xác định tọa độ các điểm mà tiếp tuyến tại đó song song với trục hoành. Lời giải a) $\frac{u}{v} \Rightarrow … [Đọc thêm...] vềĐề: a) Cho hàm số phân thức dạng $ y=\frac{u}{v}; u, v $ là hàm số của $x$ và có đạo hàm, $v(x)\neq 0$. Chứng minh rằng nếu $y'(x_0)=0$ thì $y(x_0)=\frac{u'(x_0)}{v'(x_0)} $ . b) Cho hàm số $y=\frac{x^2+x-1}{x-1} $. Xác định tọa độ các điểm mà tiếp tuyến tại đó song song với trục hoành.

Đề: Chứng minh rằng nếu hàm số $f(x)$ xác định và liên tục trên $[a;b]$ thì với các điểm $x_{1},x_{2},…,x_{n}$ bất kì thuộc $[a;b]$ đều có một số $c\in [a;b]$ sao cho $f(c)=\frac{1}{n}[f(x_{1})+f(x_{2})+…+f(x_{n})]$.

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Hàm số liên tục

Đề bài: Chứng minh rằng nếu hàm số $f(x)$ xác định và liên tục trên $[a;b]$ thì với các điểm $x_{1},x_{2},...,x_{n}$ bất kì thuộc $[a;b]$ đều có một số $c\in [a;b]$ sao cho $f(c)=\frac{1}{n}[f(x_{1})+f(x_{2})+...+f(x_{n})]$. Lời giải Nếu $x_{1},x_{2},...,x_{n}$thuộc $[a;b]$ ta có $f(x_{1})=f(x_{2})=...=f(x_{n})$ thì rõ ràng lấy $c=x_{1}\in … [Đọc thêm...] vềĐề: Chứng minh rằng nếu hàm số \(f(x)$ xác định và liên tục trên $[a;b]$ thì với các điểm $x_{1},x_{2},…,x_{n}$ bất kì thuộc $[a;b]$ đều có một số $c\in [a;b]$ sao cho $f(c)=\frac{1}{n}[f(x_{1})+f(x_{2})+…+f(x_{n})]$.

Đề: $1$. Khảo sát hàm số $y = \frac{{{x^2} + x – 5}}{{x – 2}}\left( C \right)$$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: $1$. Khảo sát hàm số $y = \frac{{{x^2} + x - 5}}{{x - 2}}\left( C \right)$$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất Lời giải $1$. Bạn đọc tự giải.$2$. Đồ thị có tiệm cận đứng $x … [Đọc thêm...] vềĐề: $1$. Khảo sát hàm số \(y = \frac{{{x^2} + x – 5}}{{x – 2}}\left( C \right)$$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất

Đề: Cho hàm số $y=-\frac{1}{3}x^2-2x^2+3x $ có đồ thị $(C)$. Viết phương trình tiếp tuyến $\Delta $ của $(C)$ tại điểm uốn và chứng minh rằng $\Delta $ là tiếp tuyến cho hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của $(C)$

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: Cho hàm số $y=-\frac{1}{3}x^2-2x^2+3x $ có đồ thị $(C)$. Viết phương trình tiếp tuyến $\Delta $ của $(C)$ tại điểm uốn và chứng minh rằng $\Delta $ là tiếp tuyến cho hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của $(C)$ Lời giải Dễ thấy điểm uốn của đồ thị là $U\left ( 2;\frac{2}{3} \right )$. Tại $U$ tiếp tuyến của $(C)$ có hệ số góc $y'(2)=-1$. Tiếp tuyến … [Đọc thêm...] vềĐề: Cho hàm số $y=-\frac{1}{3}x^2-2x^2+3x $ có đồ thị $(C)$. Viết phương trình tiếp tuyến $\Delta $ của $(C)$ tại điểm uốn và chứng minh rằng $\Delta $ là tiếp tuyến cho hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của $(C)$