Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} + 2{x^2} – mx – 10\) đồng biến trên \(\left[ {0;\, + \infty } \right)\)

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} + 2{x^2} - mx - 10\) đồng biến trên \(\left[ {0;\, + \infty } \right)\) A.\(m \ge 0\) B.\(m \le 0\) C.Không có m D.Đáp số khác Các bạn hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. … [Đọc thêm...] vềĐề: Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \frac{1}{3}{x^3} + 2{x^2} – mx – 10\) đồng biến trên \(\left[ {0;\, + \infty } \right)\)

Đề: Tìm số thực m lớn nhất để hàm số \(y = \frac{1}{3}{x^3} + \left( {1 – 2m} \right){x^2} + m + 2\) luôn đồng biến trên \(\left( {0; + \infty } \right)\).  

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Tìm số thực m lớn nhất để hàm số \(y = \frac{1}{3}{x^3} + \left( {1 - 2m} \right){x^2} + m + 2\) luôn đồng biến trên \(\left( {0; + \infty } \right)\).   A.\(m = \frac{1}{2}\) B.\(m = -\frac{1}{2}\) C.\(m = \frac{3}{2}\) D.\(m = -\frac{3}{2}\) Các bạn hãy chọn trả lời đúng trước khi … [Đọc thêm...] vềĐề: Tìm số thực m lớn nhất để hàm số \(y = \frac{1}{3}{x^3} + \left( {1 – 2m} \right){x^2} + m + 2\) luôn đồng biến trên \(\left( {0; + \infty } \right)\).  

Đề: Tìm m để hàm số \(y = \frac{x-1}{x+m}\) đồng biến trên khoảng \((2; + \infty)\)

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Tìm m để hàm số \(y = \frac{x-1}{x+m}\) đồng biến trên khoảng \((2; + \infty)\) A.\(\[ -1; + \infty)\) B.\((2; +\infty)\) C.\((-1; +\infty)\) D.\((-\infty; -2)\) Các bạn hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. Đáp án đúng: C  \(y … [Đọc thêm...] vềĐề: Tìm m để hàm số \(y = \frac{x-1}{x+m}\) đồng biến trên khoảng \((2; + \infty)\)

Đề: Hàm số \(y=\frac{mx+1}{x+m}\) đồng biến trên khoảng \((1;+\infty )\) khi:

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Hàm số \(y=\frac{mx+1}{x+m}\) đồng biến trên khoảng \((1;+\infty )\) khi: A.-1 B.m>1 C.\(m\in R \setminus \left [ -1;1 \right ]\)  D.\(m\geq 1\) Các bạn hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. Đáp án đúng: C … [Đọc thêm...] vềĐề: Hàm số \(y=\frac{mx+1}{x+m}\) đồng biến trên khoảng \((1;+\infty )\) khi:

Đề: Cho hàm số \(y=\frac{mx-8}{x-2m}\), hàm số đồng biến trên \((3;+\infty )\) khi:

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Cho hàm số \(y=\frac{mx-8}{x-2m}\), hàm số đồng biến trên \((3;+\infty )\) khi: A.\(-2\leq m\leq 2\) B. $-2< m< 2$ C.\(-2\leq m\leq \frac{3}{2}\)​ D. $-2< m\leq \frac{3}{2}$ Các bạn hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. … [Đọc thêm...] vềĐề: Cho hàm số \(y=\frac{mx-8}{x-2m}\), hàm số đồng biến trên \((3;+\infty )\) khi:

Tư duy sáng tạo tìm tòi lời giải phương trình – bất phương trình – hệ phương trình đại số vô tỷ

Ngày Thuộc chủ đề:Sách ôn thi toán Tag với:, ,

Giới thiệu sách : Tư Duy Sáng Tạo Tìm Tòi Lời Giải Phương Trình - Bất Phương Trình - Hệ Phương Trình Đại Số Vô Tỷ Tác giả Lê Văn Đoàn Số trang 773 "Chinh phục bất cứ một sự khó khăn nào luôn đem lại cho người ta một niềm vui sướng thầm lặng, bởi điều đó cũng có nghĩa là đẩy lùi một đường ranh giới và tăng thêm tự do của bản thân". Quyển … [Đọc thêm...] vềTư duy sáng tạo tìm tòi lời giải phương trình – bất phương trình – hệ phương trình đại số vô tỷ

HỆ PHƯƠNG TRÌNH ĐẠI SỐ – VÔ TỶ – Lê Văn Đoàn

Ngày Thuộc chủ đề:Sách ôn thi toán Tag với:,

HỆ PHƯƠNG TRÌNH ĐẠI SỐ – VÔ TỶ - Lê Văn Đoàn Phần 2. HỆ PHƯƠNG TRÌNH ĐẠI SỐ – VÔ TỶ Trích ra từ bài: Cẩm Nang Ôn Luyện Thi Đại Học Phương Trình – Bất Phương Trình – Hệ Phương Trình Vô Tỷ Gồm các phần sau: ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- … [Đọc thêm...] vềHỆ PHƯƠNG TRÌNH ĐẠI SỐ – VÔ TỶ – Lê Văn Đoàn

Hình 1 mô tả một chiếc đồng hồ mặt trời với một mặt đáy hình chữ nhật nghiêng so với mặt phẳng nằm ngang, trên đó có một mặt đồng hồ hình tròn. Trên mặt đáy này có gắn một chiếc cọc, bóng của cọc khi chiếu sáng sẽ chi giờ trên mặt đồng hồ

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:

Bài toán: Hình 1 mô tả một chiếc đồng hồ mặt trời với một mặt đáy hình chữ nhật nghiêng so với mặt phẳng nằm ngang, trên đó có một mặt đồng hồ hình tròn. Trên mặt đáy này có gắn một chiếc cọc, bóng của cọc khi chiếu sáng sẽ chi giờ trên mặt đồng hồ. Chiếc đồng hồ mặt trời như vậy được mô hình hóa trong một hệ tọa độ $Oxyz$ như hình 2 . Ở đây, hình chữ nhật $ABCD$ với … [Đọc thêm...] vềHình 1 mô tả một chiếc đồng hồ mặt trời với một mặt đáy hình chữ nhật nghiêng so với mặt phẳng nằm ngang, trên đó có một mặt đồng hồ hình tròn. Trên mặt đáy này có gắn một chiếc cọc, bóng của cọc khi chiếu sáng sẽ chi giờ trên mặt đồng hồ

Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi $x$ là đại diện cho phần trăm số gia đình trong một quốc gia và $y$ là phần trăm tổng thu nhập, mô hình $y=x$ sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz $y=f\left( x \right)$, biểu thị sự phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với $0\le x\le 100$, biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường cong Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số: $y={{\left( 0,00061{{x}^{2}}+0,0218x+1,723 \right)}^{2}},0\le x\le 100$ Trong đó $x$ được tính từ các gia đình nghèo nhất đến giàu có nhất Theo R.Larson, Brief Calculus: An Applied Approach, ${{8}^{\text{th }\!\!~\!\!\text{ }}}$ edition, Cengage Learning,

Ngày Thuộc chủ đề:Trắc nghiệm Tích phân Tag với:

ĐỀ BÀI Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi $x$ là đại diện cho phần trăm số gia đình trong một quốc gia và $y$ là phần trăm tổng thu nhập, mô hình $y=x$ sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz $y=f\left( x \right)$, biểu thị sự phân phối thu nhập thực tế. Diện tích giữa … [Đọc thêm...] vềCác nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi $x$ là đại diện cho phần trăm số gia đình trong một quốc gia và $y$ là phần trăm tổng thu nhập, mô hình $y=x$ sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz $y=f\left( x \right)$, biểu thị sự phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với $0\le x\le 100$, biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường cong Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số: $y={{\left( 0,00061{{x}^{2}}+0,0218x+1,723 \right)}^{2}},0\le x\le 100$ Trong đó $x$ được tính từ các gia đình nghèo nhất đến giàu có nhất Theo R.Larson, Brief Calculus: An Applied Approach, ${{8}^{\text{th }\!\!~\!\!\text{ }}}$ edition, Cengage Learning,

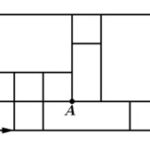
Trên đường đi từ nhà Mạnh $(M)$ đến công ty $(C)$ có điểm $A$ người ta đang thi công sửa chữa đường nên không thể đi qua vị trí điểm $A$. Biết rằng toàn bộ cung đường theo bản đồ từ dưới lên trên và từ trái qua phải là đường một chiều nên vì vậy nên Mạnh chỉ được phép đi lên hoặc đi sang phải.

Ngày Thuộc chủ đề:Toán thực tế THPT 2015 Tag với:

ĐỀ BÀI Trên đường đi từ nhà Mạnh $(M)$ đến công ty $(C)$ có điểm $A$ người ta đang thi công sửa chữa đường nên không thể đi qua vị trí điểm $A$. Biết rằng toàn bộ cung đường theo bản đồ từ dưới lên trên và từ trái qua phải là đường một chiều nên vì vậy nên Mạnh chỉ được phép đi lên hoặc đi sang phải. Vậy Mạnh có bao nhiêu cách đi từ nhà đến công ty? LỜI GIẢI ĐÁP ÁN 15 Từ … [Đọc thêm...] vềTrên đường đi từ nhà Mạnh $(M)$ đến công ty $(C)$ có điểm $A$ người ta đang thi công sửa chữa đường nên không thể đi qua vị trí điểm $A$. Biết rằng toàn bộ cung đường theo bản đồ từ dưới lên trên và từ trái qua phải là đường một chiều nên vì vậy nên Mạnh chỉ được phép đi lên hoặc đi sang phải.