Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
DẠNG TOÁN 4: BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG. 1. PHƯƠNG PHÁP GIẢI Cho $\vec a = \left( {{x_1};{y_1}} \right)$, $\vec b = \left( {{x_2};{y_2}} \right).$ Khi đó: + Tích vô hướng hai vectơ là $\vec a.\vec b = {x_1}{x_2} + {y_1}{y_2}.$ + Góc của hai vectơ được xác định bởi công thức: $\cos (\vec a,\vec b) = \frac{{\vec a.\vec b}}{{|\vec a||\vec b|}}$ $ = … [Đọc thêm...] vềBIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG
DẠNG TOÁN 3: TÌM TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VỀ TÍCH VÔ HƯỚNG HOẶC TÍCH ĐỘ DÀI. 1. PHƯƠNG PHÁP GIẢI Ta sử dụng các kết quả cơ bản sau: Cho $A$, $B$ là các điểm cố định. $M$ là điểm di động. + Nếu $|\overrightarrow {AM} | = k$ với $k$ là số thực dương cho trước thì tập hợp các điểm $M$ là đường tròn tâm $A$, bán kính $R = k.$ + Nếu $\overrightarrow {MA} … [Đọc thêm...] vềTÌM TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VỀ TÍCH VÔ HƯỚNG HOẶC TÍCH ĐỘ DÀI
DẠNG TOÁN 1: XÁC ĐỊNH GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC ĐẶC BIỆT. 1. PHƯƠNG PHÁP GIẢI + Sử dụng định nghĩa giá trị lượng giác của một góc. + Sử dụng tính chất và bảng giá trị lượng giác đặc biệt. + Sử dụng các hệ thức lượng giác cơ bản. 2. CÁC VÍ DỤ Ví dụ 1 : Tính giá trị các biểu thức sau: a) $A = {a^2}\sin {90^0} + {b^2}\cos {90^0} + {c^2}\cos {180^0}.$ b) $B = 3 – … [Đọc thêm...] vềXÁC ĐỊNH GIÁ TRỊ LƯỢNG GIÁC CỦA GÓC ĐẶC BIỆT
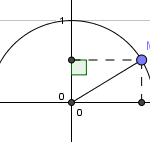
Lý thuyết Bài Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ Trước khi đi vào định nghĩa, ta xét hình sau: Hình trên mô phỏng một nửa đường tròn có bán kín bằng 1. Ta gọi nó là nửa đường tròn đơn vị . Điểm M thuộc nửa đường tròn ấy, vậy góc cho trước có độ lớn từ 0 độ đến 180 độ. 1. Định nghĩa Với mỗi góc \(\alpha(0^o\leq \alpha\leq 180^o)\), ta xác … [Đọc thêm...] vềLý thuyết Bài Giá trị lượng giác của một góc bất kỳ từ 0 đến 180 độ
DẠNG TOÁN 2: SỬ DỤNG BẤT ĐẲNG THỨC CAUCHY(côsi) ĐỂ CHỨNG MINH BẤT ĐẲNG THỨC VÀ TÌM GIÁ TRI LỚN NHẤT, NHỎ NHẤT 1. Phương pháp giải Một số chú ý khi sử dụng bất đẳng thức côsi: * Khi áp dụng bđt côsi thì các số phải là những số không âm * BĐT côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích * Điều kiện xảy ra dấu ‘=’ là các số bằng nhau * Bất … [Đọc thêm...] vềBất đẳng thức – SỬ DỤNG BẤT ĐẲNG THỨC CAUCHY
1. Phép biến hình - Điểm \(M'\) gọi là ảnh của điểm \(M\) qua phép biến hình \(F\) , hay \(M\) là điểm tạo ảnh của điểm \(M'\), kí hiệu \(M' = f\left( M \right)\) - Nếu \(\left( H \right)\) là một hình nào đó thì \(\left( {H'} \right)\) gồm các điểm \(M'\) là ảnh của \(M \in {\rm H}\) được gọi là ảnh của \(\left( {\rm H} \right)\) qua phép biến hình \(F\) . - Phép biến … [Đọc thêm...] vềÔn Chương 1 – Hình học 11
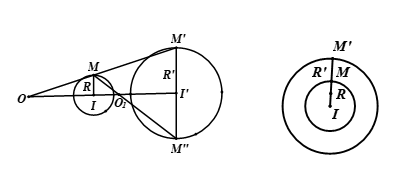
1. Định nghĩa Phép biến hình \(F\) được gọi là phép đồng dạng tỉ số \(k\left( {k > 0} \right)\) nếu với hai điểm \(M,N\) bất kì và ảnh \(M',N'\) của chúng ta luôn có \(M'N' = k.MN\). - Phép dời hình là phép đồng dạng tỉ số \(k = 1\). - Phép vị tự tỉ số \(k\) là phép đồng dạng tỉ số \(\left| k \right|\). - Nếu thực hiện liên tiếp các phép đồng dạng thì được một … [Đọc thêm...] vềBài 8: Phép đồng dạng – Chương 1 – Hình học 11
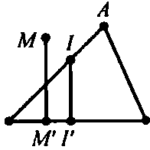
1. Định nghĩa Cho điểm \(I\) và một số thực \(k \ne 0\). Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\overrightarrow {IM'} = k.\overrightarrow {IM} \) được gọi là phép vị tự tâm \(I\) tỉ số \(k\). Kí hiệu \({V_{\left( {I;k} \right)}}\). 2. Tính chất - Nếu ${V_{\left( {I;k} \right)}}\left( M \right) = M',{V_{\left( {I;k} \right)}}\left( N \right) = … [Đọc thêm...] vềBài 7: Phép vị tự – Chương 1 – Hình học 11
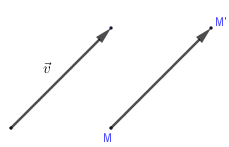
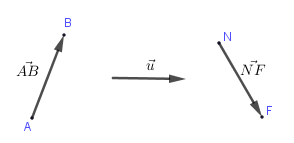
1. Định nghĩa vectơ Vectơ là đoạn thẳng có hướng, nghĩa là trong hai điểm mút của đoạn thẳng đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối. Vectơ có điểm đầu là $A,$ điểm cuối là $B$ ta kí hiệu $\overrightarrow {AB} $ Vectơ còn được kí hiệu là: $\overrightarrow a ,{\rm{ }}\overrightarrow b ,{\rm{ }}\overrightarrow x ,{\rm{ }}\overrightarrow y ,...$ Vectơ – … [Đọc thêm...] vềBài 1. Các định nghĩa Vecto – Chương 1 – Hình học 10
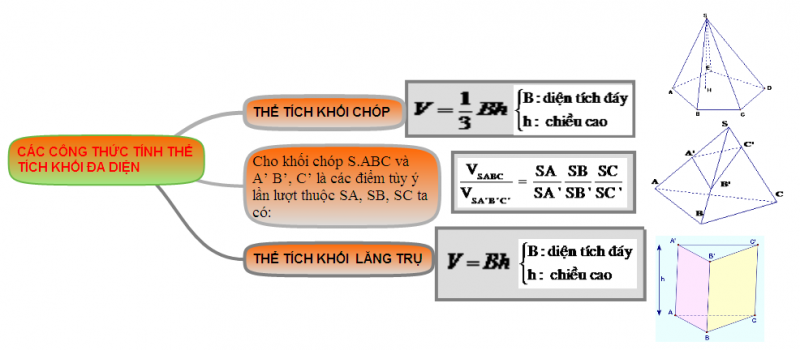
Sơ đồ các công thức tính thể tích khối đa diện Sơ đồ phân loại các dạng toán về thể tích Bài tập minh họa Bài tập 1: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh \(2a\sqrt{2}\) và \(AA’=a\sqrt{3}\). Hình chiếu vuông góc của điểm A’ trên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC. Tính theo a thể tích khối lăng trụ ABC.A’B’C’ và … [Đọc thêm...] vềÔn tập chương I Khối đa diện
