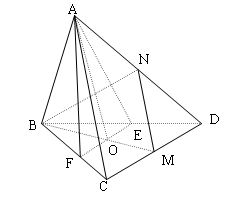
Đề bài: Cho hình tứ diện đều $ABCD$ cạnh $a$. Gọi $O$ là tâm đường tròn ngoại tiếp $\Delta BCD$$a.$ Chứng minh rằng $AO$ vuông góc với $CD$$b.$ Gọi $M$ là trung điểm $CD$. Tính góc giữa $AC,BM$

Lời giải

$a.$ Qua $O$ dựng đường thẳng song song với $CD$ cắt $BC,BD$ theo thứ tự tại $E,F$ suy ra:
$(AO,CD)=\widehat{AOF} $
Ta có :
$\begin{cases} EF//CD\\BC=BD\\MC=MD\end{cases} \Leftrightarrow \begin{cases}BE=BF\\OE=Ò \end{cases} $
Xét hai tam giác $\Delta ABE$ và $\Delta ABF$ ta có :
$\begin{cases}BE=BF\\AB chung\\\widehat{ABE}=\widehat{ABF}=60^0 \end{cases} \Rightarrow \Delta ABE=\Delta ABF\Rightarrow AE=AF$
$\Leftrightarrow \Delta AEF$ cân tại $A\Rightarrow AO\bot EF\Leftrightarrow \widehat{AOF} =90^0\Leftrightarrow AO\bot CD$
$b.$ Bạn đọc tự giải- ĐS : $\frac{\sqrt{3} }{6} $
