Cho hình hộp \(ABCD.A’B’C’D’\) có thể tích \(V\). Gọi \(G\) là trọng tâm tam giác \(AC’D\), \(E\) là trung điểm \(A’D’\). Tính thể tích khối chóp \(AEGC’\) theo \(V\).

Cho hình hộp \(ABCD.A’B’C’D’\) có thể tích \(V\). Gọi \(G\) là trọng tâm tam giác \(AC’D\), \(E\) là trung điểm \(A’D’\). Tính thể tích khối chóp \(AEGC’\) theo \(V\).

A. \(\frac{V}{{12}}.\).

B. \(\frac{V}{9}.\).

C. \(\frac{V}{{16}}.\).

D. \(\frac{V}{{18}}.\)

Lời giải:

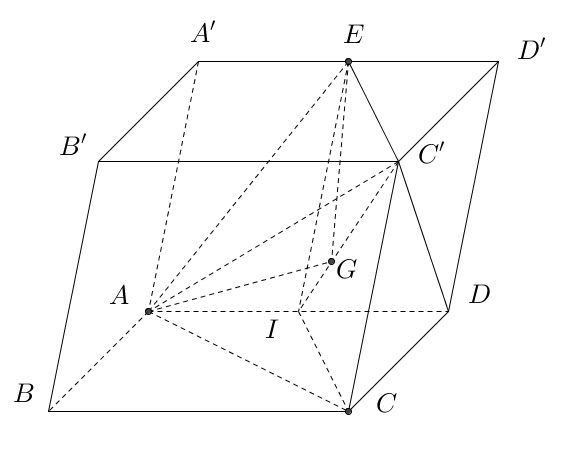
Gọi \(I\) là trung điểm \(AD\).

\({V_{A.EC’G}} = {V_{D.EC’G}} = \frac{1}{3}{V_{D.ICC’E}} = \frac{1}{3}.\frac{2}{3}.\frac{1}{4}V = \frac{V}{{18}}\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Thể tích đa diện.