Cho chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), vuông cân tại A, \(BC = a\sqrt 2 \). Biết khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(\frac{{a\sqrt 3 }}{3}\). Tính thể tích khối chóp \(S.ABC\)

Cho chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), vuông cân tại A, \(BC = a\sqrt 2 \). Biết khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(\frac{{a\sqrt 3 }}{3}\). Tính thể tích khối chóp \(S.ABC\)

A. \(\frac{{{a^3}}}{2}\).

B. \(\frac{{{a^3}}}{6}\).

C. \(\frac{{3{a^3}\sqrt 2 }}{{16}}\).

D. \(\frac{{3{a^3}\sqrt 2 }}{{48}}\).

Lời giải:

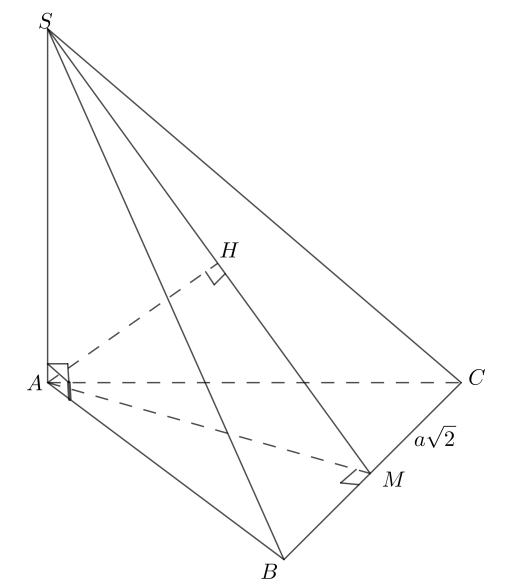
Kẻ \(AM \bot BC,AH \bot SM\).

+ Ta có \(\left. \begin{array}{l}BC \bot AM\\BC \bot SA\\SA,AM \subset \left( {SAM} \right)\end{array} \right\} \Rightarrow BC \bot \left( {SAM} \right)\)

mà \(AH \in \left( {SAM} \right) \Rightarrow BC \bot AH\).

+ Ta có \(\left. \begin{array}{l}AH \bot SM\\AH \bot BC\\SM,BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow d\left( {A;\left( {SBC} \right)} \right) = AH = \frac{{a\sqrt 3 }}{3}\).

+ AM là đường trung tuyến trong tam giác vuông ABC nên \(AM = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}\)

+ Xét tam giác vuông \(SAM\) có \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{M^2}}} \Rightarrow \frac{1}{{S{A^2}}} = \frac{3}{{{a^2}}} – \frac{2}{{{a^2}}} = \frac{1}{{{a^2}}}\) \( \Rightarrow SA = a\)

+ Thể tích khối chóp là \(V = \frac{1}{3}{S_{ABC}}.SA = \frac{1}{3}\left( {\frac{1}{2}\frac{{a\sqrt 2 }}{2}.a\sqrt 2 } \right).a = \frac{{{a^3}}}{6}\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Thể tích đa diện.