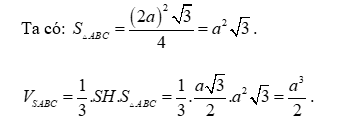Cho hình chóp \(S.ABC\) có \(\Delta ABC\) đều; mặt bên \(SAB\) nằm trong mặt phẳng vuông góc với mặt đáy và \(\Delta SAB\) vuông tại \(S\), \(SA = a\sqrt 3 \), \(SB = a\). Tính thể tích khối chóp \(S.ABC\).

Cho hình chóp \(S.ABC\) có \(\Delta ABC\) đều; mặt bên \(SAB\) nằm trong mặt phẳng vuông góc với mặt đáy và \(\Delta SAB\) vuông tại \(S\), \(SA = a\sqrt 3 \), \(SB = a\). Tính thể tích khối chóp \(S.ABC\).

A. \(\frac{{{a^3}}}{4}\).

B. \(\frac{{{a^3}}}{3}\).

C. \(\frac{{{a^3}}}{6}\).

D. \(\frac{{{a^3}}}{2}\).

Lời giải:

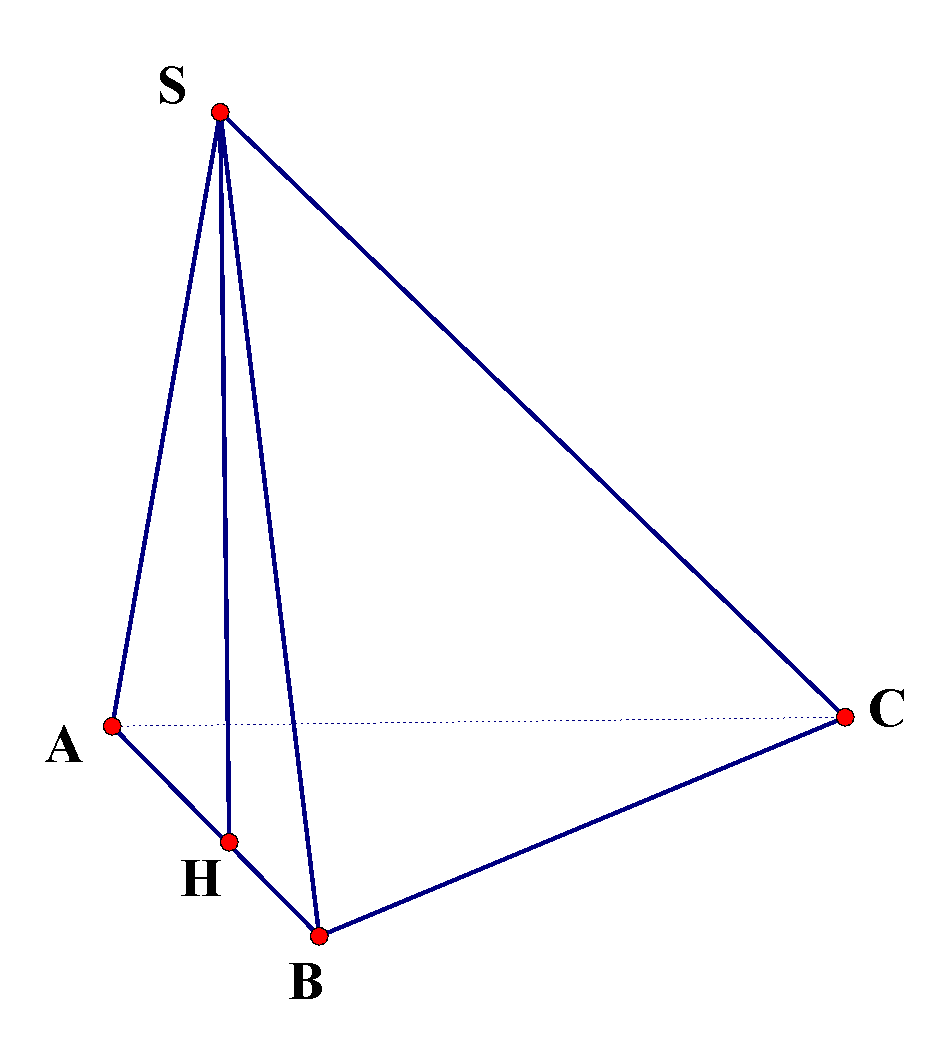
Kẻ \(SH\) vuông góc với \(AB\) tại \(H\). Ta có \(SH \bot \left( {ABC} \right)\)

Áp dụng định lý Pi – ta – go trong \(\Delta SAB\) vuông tại \(S\), ta có: \(AB = \sqrt {S{A^2} + S{B^2}} = \sqrt {4{a^2}} = 2a\). Áp dụng hệ thức lượng trong \(\Delta SAB\) vuông tại \(S\) có đường cao \(SH\), ta có:

\(SH = \frac{{SA.SB}}{{AB}} = \frac{{a\sqrt 3 .a}}{{2a}} = \frac{{a\sqrt 3 }}{2}\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Thể tích đa diện.