Cho hàm số $y=f\left( x \right)$ liên tục trên D và có đạo hàm ${f}’\left( x \right)={{\left( x+1 \right)}^{2}}{{\left( x-1 \right)}^{3}}\left( 2-x \right)$. Hàm số $y=f\left( x \right)$ đồng biến trên khoảng $\left( a;b \right)$.

Đáp án: 0,5

Lời giải:

Đáp án: 0,5 Ta có ${f}’\left( x \right)=0\Leftrightarrow {{\left( x+1 \right)}^{2}}{{\left( x-1 \right)}^{3}}\left( 2-x \right)=0\Leftrightarrow \left[ \begin{array}{l} x=-1 \\ x=1 \\ x=2 \end{array} \right.$. Lập bảng xét dấu của ${f}’\left( x \right)$ ta được:

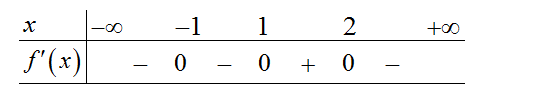
Từ bảng xét dấu ta có hàm số $y=f\left( x \right)$ đồng biến trên khoảng $\left( 1;2 \right)$. Suy ra $a=1$, $b=2$. Vậy $\dfrac{a}{b}=\dfrac{1}{2}=0,5$.