Câu 46: (MH Toan 2020) Cho hàm số bậc bốn \(y = f(x)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g(x) = f\left( {{x^3} + 3{x^2}} \right)\) là

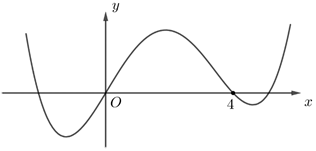
Câu 46: (MH Toan 2020) Cho hàm số bậc bốn \(y = f(x)\) có đồ thị như hình bên. Số điểm cực trị của hàm số \(g(x) = f\left( {{x^3} + 3{x^2}} \right)\) là
A. \(5\).
B. \(3\).
C. \(7\).
D. \(11\).

Lời giải
Đáp án: C
Từ đồ thị, ta có bảng biến thiên của \(y = f(x)\) như sau:

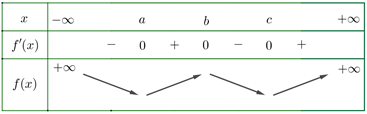
Ta có \(g(x) = f\left( {{x^3} + 3{x^2}} \right) \Rightarrow g\prime (x) = \left( {3{x^2} + 6x} \right).f\prime \left( {{x^3} + 3{x^2}} \right)\).
Cho \(g\prime (x) = 0 \Leftrightarrow \left[ \begin{array}{l}3{x^2} + 6x = 0\\f\prime \left( {{x^3} + 3{x^2}} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = – 2\\{x^3} + 3{x^2} = a;\;a < 0\\{x^3} + 3{x^2} = b;\;0 < b < 4\\{x^3} + 3{x^2} = c;\;c > 4\end{array} \right.\)
Xét hàm số \(h(x) = {x^3} + 3{x^2}\) \( \Rightarrow h\prime (x) = 3{x^2} + 6x\)\( \Rightarrow h\prime (x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = – 2\end{array} \right.\)
Bảng biến thiên

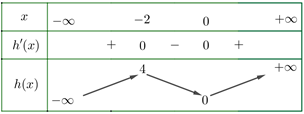
Từ bảng biến thiên, ta thấy
Đường thẳng $y=a$ cắt đồ thị hàm số $y=h(x)$ tại 1 điểm
Đường thẳng $y=b$ cắt đồ thị hàm số $y=h(x)$ tại 3 điểm.
Đường thẳng $y=c$ cắt đồ thị hàm số $y=h(x)$ tại 1 điểm.
Như vậy, phương trình $g\prime(x)=0$ có tất cả 7 nghiệm đơn phân biệt.
Vậy hàm số $g(x)=f\left(x^3+3x^2\right)$ có 7 cực trị