Câu hỏi: 35. Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \frac{{{x^3}}}{{\sqrt {{x^2} + 1} }}\). Khẳng định nào dưới đây đúng? A. \(F\left( x \right) = \sqrt {{{\left( {{x^2} + 1} \right)}^3}}  + \sqrt {{x^2} + 1} \). B. \(F\left( x \right) = \sqrt {{{\left( {{x^2} + 1} \right)}^3}}  - \sqrt {{x^2} + 1} \). C. \(F\left( … [Đọc thêm...] về35. Biết \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \frac{{{x^3}}}{{\sqrt {{x^2} + 1} }}\). Khẳng định nào dưới đây đúng?

Câu hỏi: 83. Biết \(\int_{\ln \sqrt 3 }^{\ln \sqrt 8 } {\frac{1}{{\sqrt {{{\rm{e}}^{2x}} + 1}  - {{\rm{e}}^x}}}} {\rm{d}}x = 1 + \frac{1}{2}\ln \frac{b}{a} + a\sqrt a  - \sqrt b {\rm{ }}\)  với \(a,b \in {\mathbb{Z}^ + }\). Tính \(P = a + b\)? A. \(P =  - 1\). B. \(P = 1\). C. \(P = 3\). D. \(P = 5\). Lời giải Ta có: \(I = … [Đọc thêm...] về83. Biết \(\int_{\ln \sqrt 3 }^{\ln \sqrt 8 } {\frac{1}{{\sqrt {{{\rm{e}}^{2x}} + 1}  – {{\rm{e}}^x}}}} {\rm{d}}x = 1 + \frac{1}{2}\ln \frac{b}{a} + a\sqrt a  – \sqrt b {\rm{ }}\)  với \(a,b \in {\mathbb{Z}^ + }\).

Câu hỏi: 45. Cho tích phân \(I = \int_0^{1011} {{{\left( {2x - 1} \right)}^{2022}}{\rm{d}}x} \). Đặt \(t = 2x - 1\), khẳng định nào sau đây đúng? A. \(I = \frac{1}{2}\int_0^{1011} {{t^{2022}}{\rm{d}}t} \). B. \(\frac{1}{2}\int_{ - 1}^{2021} {{t^{2022}}{\rm{d}}t} \). C. \(I = \int_{ - 1}^{2021} {{t^{2022}}{\rm{d}}t} \). D. \(I = \int_0^{1011} … [Đọc thêm...] về45. Cho tích phân \(I = \int_0^{1011} {{{\left( {2x – 1} \right)}^{2022}}{\rm{d}}x} \). Đặt \(t = 2x – 1\), khẳng định nào sau đây đúng?

Câu hỏi: 82.   Cho \(\int\limits_0^{\frac{\pi }{4}} {\frac{{4{\rm{co}}{{\rm{s}}^3}x}}{{1 + \sin x}}\,{\rm{d}}x}  = a\sqrt b  - 1\) với \(a,b \in \mathbb{Z}\). Tính \(T = ab\). A. \(T = 1\). B. \(T = 2\). C. \(T = 3\). D. \(T = 4\). Lời giải Ta có: \(I = \int\limits_0^{\frac{\pi }{4}} {\frac{{4{\rm{co}}{{\rm{s}}^2}x.\,{\rm{cos}}x}}{{1 + \sin … [Đọc thêm...] về82.   Cho \(\int\limits_0^{\frac{\pi }{4}} {\frac{{4{\rm{co}}{{\rm{s}}^3}x}}{{1 + \sin x}}\,{\rm{d}}x}  = a\sqrt b  – 1\) với \(a,b \in \mathbb{Z}\). Tính \(T = ab\).

Câu hỏi: 97. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ { - 1{\mkern 1mu} ;{\mkern 1mu} 0} \right\}\) thỏa mãn \(f\left( 1 \right) = 2\ln 2 + 1\), \(x\left( {x + 1} \right)f'\left( x \right) + \left( {x + 2} \right)f\left( x \right) = x\left( {x + 1} \right)\), \(\forall x \in \mathbb{R}\backslash \left\{ { - 1{\mkern 1mu} ;{\mkern … [Đọc thêm...] về97. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\backslash \left\{ { – 1{\mkern 1mu} ;{\mkern 1mu} 0} \right\}\) thỏa mãn \(f\left( 1 \right) = 2\ln 2 + 1\), \(x\left( {x + 1} \right)f’\left( x \right) + \left( {x + 2} \right)f\left( x \right) = x\left( {x + 1} \right)\), \(\forall x \in \mathbb{R}\backslash \left\{ { – 1{\mkern 1mu} ;{\mkern 1mu} 0} \right\}\). Biết \(f\left( 2 \right) = a + b\ln 3\), với \(a\), \(b\) là hai số hữu tỉ. Tính \(T = {a^2} – b\).

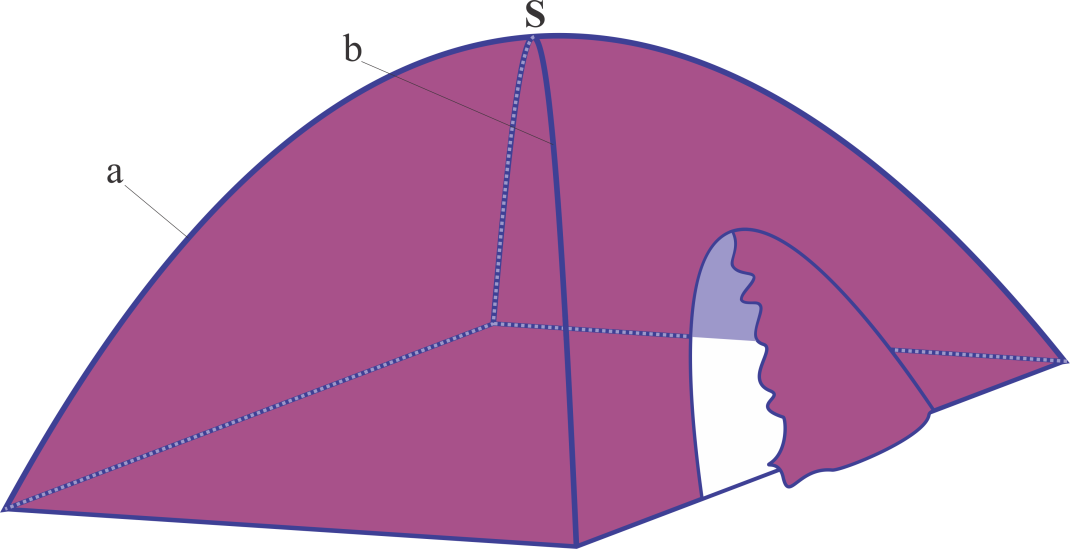
Câu hỏi: 100. Một chiếc lều vải du lịch dạng hình cong như hình bên . Khung chính bao gồm đáy là hình vuông cạnh \(2\,{\rm{m}}\) và hai xương dây \(a\), \(b\) nằm trên các đường parabol đỉnh \(S\). Biết chiều cao của lều là \(SO = 135\,{\rm{cm}}\), \(O\) là tâm của đáy. Tính thể tích chiếc lều .  A. \(\frac{{27}}{{10}}\). B. \(\frac{{26}}{9}\). C. … [Đọc thêm...] về100. Một chiếc lều vải du lịch dạng hình cong như hình bên . Khung chính bao gồm đáy là hình vuông cạnh \(2\,{\rm{m}}\) và hai xương dây \(a\), \(b\) nằm trên các đường parabol đỉnh \(S\). Biết chiều cao của lều là \(SO = 135\,{\rm{cm}}\), \(O\) là tâm của đáy. Tính thể tích chiếc lều . 

Câu hỏi: 29. Tính thể tích \(V\) của vật thể giới hạn bởi hai mặt phẳng \(x = 1\) và \(x = 3\) biết rằng thiết diện của vật thể cắt bới mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {1 \le x \le 3} \right)\) là hình vuông có cạnh \(\sqrt {3 - x} \). A. \(V = 1\). B. \(V = 2\). C. \(V = \pi \). D. \(V = 2\pi \). Lời giải Diện tích … [Đọc thêm...] về29. Tính thể tích \(V\) của vật thể giới hạn bởi hai mặt phẳng \(x = 1\) và \(x = 3\) biết rằng thiết diện của vật thể cắt bới mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {1 \le x \le 3} \right)\) là hình vuông có cạnh \(\sqrt {3 – x} \).

Câu hỏi: 21. Tính tích phân \(I = \int\limits_0^1 {3{{\rm{e}}^{{x^3} + 1}}} .{x^2}{\rm{d}}x\) bằng cách đổi biến đặt \({x^3} + 1 = u\) thì \(I\) bằng A. \(\int\limits_1^2 {{{\rm{e}}^u}} {\rm{d}}u\). B. \(\int\limits_0^1 {{{\rm{e}}^u}} {\rm{d}}u\). C. \(3\int\limits_0^1 {{{\rm{e}}^u}} {\rm{d}}u\). D. \(3\int\limits_1^2 {{{\rm{e}}^u}} {\rm{d}}u\). Lời … [Đọc thêm...] về21. Tính tích phân \(I = \int\limits_0^1 {3{{\rm{e}}^{{x^3} + 1}}} .{x^2}{\rm{d}}x\) bằng cách đổi biến đặt \({x^3} + 1 = u\) thì \(I\) bằng

Câu hỏi: 31. Biết hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \cos 2x\) và thoả mãn \(F\left( \pi  \right) = 1\). Giá trị của \(F\left( {\frac{\pi }{4}} \right)\) bằng A. \(1\). B. \(\frac{3}{2}\). C. \(2\). D. \(\frac{1}{2}\). Lời giải Ta có \(\int {f\left( x \right){\rm{d}}x}  = \int {\cos 2x} {\rm{d}}x\)\( … [Đọc thêm...] về31. Biết hàm số \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \cos 2x\) và thoả mãn \(F\left( \pi  \right) = 1\). Giá trị của \(F\left( {\frac{\pi }{4}} \right)\) bằng

Câu hỏi: 78: Cho \(f\left( x \right)\) và \(g\left( x \right)\) là hai hàm số liên tục trên \(\mathbb{R}\). Biết \(\int\limits_{ - 1}^5 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]{\rm{d}}x}  = 16\) và \(\int\limits_{ - 1}^5 {\left[ {f\left( x \right) - 3g\left( x \right)} \right]{\rm{d}}x}  =  - 1\). Tính \(I = \int\limits_{ - 1}^2 {f\left( … [Đọc thêm...] về78: Cho \(f\left( x \right)\) và \(g\left( x \right)\) là hai hàm số liên tục trên \(\mathbb{R}\). Biết \(\int\limits_{ – 1}^5 {\left[ {2f\left( x \right) + 3g\left( x \right)} \right]{\rm{d}}x}  = 16\) và \(\int\limits_{ – 1}^5 {\left[ {f\left( x \right) – 3g\left( x \right)} \right]{\rm{d}}x}  =  – 1\). Tính \(I = \int\limits_{ – 1}^2 {f\left( {2x + 1} \right){\rm{d}}x} \).