Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
Gồm các bài học sau (gồm có phần nâng cao và cơ bản): ============= Mời các bạn chọn phần cần đọc. =========== Lý thuyết Khái niệm về khối đa diện Khối đa diện là gì? Ví dụ minh họa khái niệm khối đa diện Phân chia và lắp ghép khối đa diện Trắc nghiệm Khái niệm về khối đa diện Giải bài tập Bài 1 Khối đa diện – SGK hình học 12 cơ bản Chương I. … [Đọc thêm...] vềBài 1 Khái niệm về khối đa diện
Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt Mỗi đỉnh của hình đa diện là dỉnh chung của ít nhất bao nhiêu mặt A. 2 mặt B. 3 mặt C. 4 mặt D. 5 mặt ================= Đáp án đúng: B … [Đọc thêm...] vềMỗi đỉnh của hình đa diện là đỉnh chung của ít nhất bao nhiêu mặt
Cho bốn hình sau đây: Khẳng định nào sau đây sai? Cho bốn hình sau đây: Khẳng định nào sau đây sai? A. Khối đa diện A không phải là khối đa diện đều B. Khối đa diện B là khối đa diện lồi C. Khối đa diện C là khối đa diện lồi D. Cả 4 khối đa diện A, B, C, D đều là khối đa diện lồi. --------------- Đáp án đúng: D Nhắc lại khái niệm “đa diện … [Đọc thêm...] vềCho bốn hình sau đây: Khẳng định nào sau đây sai?
Hình lăng trụ có thể có số cạnh là số nào sau đây? A. 2015 B. 2017 C. 2018 D. 2016 Đáp án đúng: D Nếu hình lăng trụ có đáy là đa giác n cạnh thì số cạnh đáy của hình lăng trụ là 2n và số cạnh bên là n ⇒ tổng số cạnh của hình lăng trụ là 3n. Vậy số cạnh của hình lăng trụ là một số chia hết cho 3. ⇒ Loại A, B, C D đúng vì 2016 chia hết cho … [Đọc thêm...] vềHình lăng trụ có thể có số cạnh là số nào sau đây?
Trắc nghiệm Khái niệm về khối đa diện Các bạn xem mục lục bên dưới: … [Đọc thêm...] vềTrắc nghiệm Khái niệm về khối đa diện
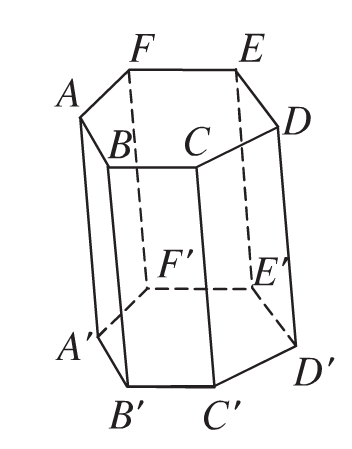
Lý thuyết Khái niệm về khối đa diện 1) Khối lăng trụ Hình lăng trụ: 2 đáy là 2 đa giác bằng nhau. Các cạch bên song song và bằng nhau. Các mặt bên là các hình bình hành. Khối lăng trụ là phần không gian giới hạn bởi hình lăng trụ. Hình lăng trụ đứng: Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt … [Đọc thêm...] vềLý thuyết Khái niệm về khối đa diện
Bài tập minh họa Bài tập 1: Cho hàm số: \(y=\frac{1}{3}x^3-mx^2+(m^2-m+1)x+1\). Tìm m để hàm số: a) Có cực đại và cực tiểu. b) Đạt cực đại tại điểm x=1. Lời giải: TXĐ: \(D=\mathbb{R}.\) Đạo hàm: \(y’=x^2-2mx+m^2-m+1\). a) Tìm m để hàm số có cực đại và cực tiểu. Hàm số có cực đại và cực tiểu khi và chỉ khi: y’=0 có 2 nghiệm phân biệt. Điều này xảy ra … [Đọc thêm...] vềVí dụ Ôn tập chương I Giải tích 12
1. Kiến thức cần nhớ Sự đơn điệu của hàm số. Cực trị của hàm số. Giá trị lớn nhất – Giá trị nhỏ nhất của hàm số. Tiệm cận của đồ thị hàm số. Khảo sát sự biến thiên và vẽ đồ thị hàm số. 2. Các dạng toán thường gặp a) Một số dạng toán về sự đơn điệu của hàm số thường gặp Dạng 1: Xét tính đơn điệu của hàm số Dạng 2: Định giá trị của tham số m để … [Đọc thêm...] vềLý thuyết Ôn tập chương I Giải tích 12
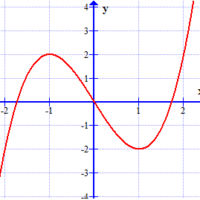
Sự tương giao của đồ thị - Sự tương giao của đường cong... Sự tương giao của hai đồ thị: Hoành độ giao điểm của 2 đồ thị hàm số $y = f(x)$ và $y = g(x)$ là nghiệm của phương trình: $$f(x) = g(x), \ \ \ (*)$$ Từ đó suy ra số giao điểm của hai đồ thị đã cho bằng số nghiệm của phương trình $(*)$. ------------- 1. Dựa vào đồ thị để biện luận số nghiệm của phương trình: … [Đọc thêm...] vềSự tương giao của đồ thị
Đây là bài toán trong phần khảo sát hàm số Viết phương trình tiếp tuyến tại một điểm thuộc đồ thị Bài toán 1 : Cho hàm số $y = f(x)$ có đồ thị $(C)$ và điểm ${M_0}\left( {{x_0};{y_0}} \right) \in (C).$ Viết phương trình tiếp tuyến của đồ thị $(C)$ tại điểm ${M_0}\left( {{x_0};{y_0}} \right) \in (C).$ Phương pháp giải : + Tiếp tuyến tại một điểm ${M_0}\left( … [Đọc thêm...] vềPhương trình tiếp tuyến của hàm số
