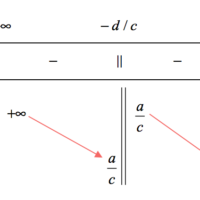
Khảo sát và vẽ đồ thị hàm nhất biến. Khảo sát và vẽ đồ thị hàm bậc nhất trên bậc nhất. Hàm nhất biến. Có dạng $y = \frac{{ax + b}}{{cx + d}},\;\;ad \ne bc.$ $\left( a \right)$ Tập xác định $D = \mathbb{R}\backslash \left\{ { - \frac{d}{c}} \right\}$. $\left( b \right)$ Giới hạn và tiệm cận: $\left( b_1 \right)$ $\mathop {\lim }\limits_{x \to {{\left( { - \frac{d}{c}} … [Đọc thêm...] vềKhảo sát sự biến thiên và vẽ đồ thị của hàm nhất biến
Khảo sát sự biến thiên và vẽ đồ thị của hàm trùng phương
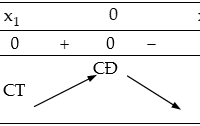
Phương pháp : Các bước khảo sát và vẽ đồ thị hàm số trùng phương $y = a{x^4} + b{x^2} + c$ với $a ≠ 0.$ + Bước 1. TXĐ: $D=\mathbb{R}.$ + Bước 2. Đạo hàm: ${y}’=4a{{x}^{3}}+2bx$ $=2x(2a{{x}^{2}}+b)$ $\Rightarrow {y}’=0\Leftrightarrow x=0$ hoặc ${{x}^{2}}=-\frac{b}{2a}$. Nếu $ab\ge 0$ thì $y$ có một cực trị ${{x}_{0}}=0.$ Nếu $ab<0$ thì $y$ có $3$ cực trị … [Đọc thêm...] vềKhảo sát sự biến thiên và vẽ đồ thị của hàm trùng phương
Khảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba
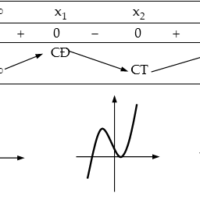
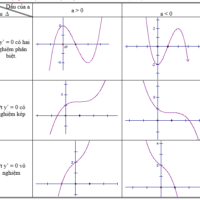
Phương pháp : Các bước khảo sát và vẽ đồ thị hàm số bậc ba $y = a{x^3} + b{x^2} + cx + d$ với $a ≠ 0.$ + Bước 1. Tập xác định: $D = R.$ + Bước 2. Đạo hàm: $y’ = 3a{x^2} + 2bx + c$, $\Delta’ = {b^2} – 3ac.$ $\Delta’ > 0$: Hàm số có $2$ cực trị. $\Delta’ \le 0$: Hàm số luôn tăng hoặc luôn giảm trên $R$. + Bước 3. Đạo hàm cấp $2$: $y” = 6ax + 2b$, $y” = 0 \Leftrightarrow x … [Đọc thêm...] vềKhảo sát sự biến thiên và vẽ đồ thị của hàm số bậc ba
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số a) Sơ đồ chung các bước khảo sát sự biến thiên và vẽ đồ thị hàm số Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y=f(x)\): Bước 1: Tìm tập xác định của hàm số Bước 2: Khảo sát sự biến thiên: Xét chiều biến thiên của hàm số: Tính đạo hàm \(f'(x)\). Tìm các điểm mà tại đó \(f'(x)=0\) hoặc không xác định. … [Đọc thêm...] vềLý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Ví dụ Đường tiệm cận
Phương pháp Tìm tiệm cận ngang, tiệm cận đứng của đồ thị hàm số $y = f(x)$ Thực hiện theo các bước sau: + Bước 1. Tìm tập xác định của hàm số $f(x).$ + Bước 2. Tìm các giới hạn của $f(x)$ khi $x$ dần tới các biên của miền xác định và dựa vào định nghĩa của các đường tiệm cận để kết luận. Chú ý: + Đồ thị hàm số $f$ chỉ có thể có tiệm cận ngang khi tập xác định của nó là … [Đọc thêm...] vềVí dụ Đường tiệm cận
Lý thuyết Đường tiệm cận
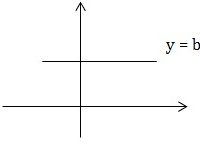
1. Đường tiệm cận ngang a) Định nghĩa Đường thẳng \(y=b\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau: \(\lim_{x\rightarrow -\infty } f(x) = b\) \(\lim_{x\rightarrow +\infty } f(x) = b\) b) Chú ý Điều kiện để đồ thị hàm số \(y = \frac{P(x)}{Q(x)}\) có tiệm cận ngang là bậc của đa thức P(x) bé hơn … [Đọc thêm...] vềLý thuyết Đường tiệm cận
Đề thi thử 2019 môn Toán – trường THPT chuyên Bắc Ninh lần 1
Đề thi thử 2019 môn Toán - trường THPT chuyên Bắc Ninh lần 1 ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- … [Đọc thêm...] vềĐề thi thử 2019 môn Toán – trường THPT chuyên Bắc Ninh lần 1
Toán học tuổi trẻ – số 495 tháng 09/2018
Toán học tuổi trẻ – số 495 tháng 09/2018 ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- … [Đọc thêm...] vềToán học tuổi trẻ – số 495 tháng 09/2018
Toán học tuổi trẻ – số 494 tháng 08/2018
Toán học tuổi trẻ – số 494 tháng 08/2018 Toán học tuổi trẻ năm 2018 ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- … [Đọc thêm...] vềToán học tuổi trẻ – số 494 tháng 08/2018
Toán học tuổi trẻ – số 493 tháng 07/2018
Toán học tuổi trẻ – số 493 tháng 07/2018 Toán học tuổi trẻ năm 2018 Chúc phát triển..... có nhiều đề thi thử toán hay. ------------- các bạn xem online và tải về: ------------------ -------------- DOWNLOAD HERE -------------- … [Đọc thêm...] vềToán học tuổi trẻ – số 493 tháng 07/2018