1. Đường tiệm cận ngang
a) Định nghĩa
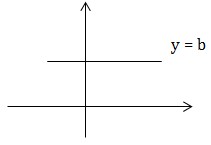
Đường thẳng \(y=b\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau:
- \(\lim_{x\rightarrow -\infty } f(x) = b\)
- \(\lim_{x\rightarrow +\infty } f(x) = b\)

b) Chú ý
- Điều kiện để đồ thị hàm số \(y = \frac{P(x)}{Q(x)}\) có tiệm cận ngang là bậc của đa thức P(x) bé hơn hoặc bằng bậc của đa thức Q(x).
- Tổng quát: Xét hàm số \(y = \frac{a_nx^n + … + a_0}{b_mx^m + … + b_0} \ \ \ m, n \in N; a_n\neq 0; b_m\neq 0\).
- Điều kiện để hàm số có tiệm cận ngang là \(n\leq m.\)
- Nếu \(n=m\): tiệm cận ngang là đường thẳng \(y = \frac{a_n}{b_m}\)
- Nếu \(n<m\) tiệm cận ngang là đường thẳng \(y=0.\)
2. Đường tiệm cận đứng
a) Định nghĩa
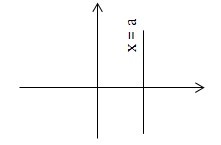
Đường thẳng \(x=a\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau:
- \(\lim_{x\rightarrow a^+} f(x) = \pm \infty\)
- \(\lim_{x\rightarrow a^-} f(x) = \pm \infty\)
b) Chú ý
- Đường thẳng \(x=a\) là đường tiệm cận đứng của đồ thị \(y = f(x)\) thì a không thuộc tập xác định của \(f(x)\).
- Đối với hàm phân thức \(y = \frac{P(x)}{Q(x)}\) thì a là nghiệm Q(x)=0.
Phương pháp
1. Tìm tiệm cận ngang, tiệm cận đứng của đồ thị hàm số $y = f(x)$
Thực hiện theo các bước sau:
+ Bước 1. Tìm tập xác định của hàm số $f(x).$
+ Bước 2. Tìm các giới hạn của $f(x)$ khi $x$ dần tới các biên của miền xác định và dựa vào định nghĩa của các đường tiệm cận để kết luận.
Chú ý:
+ Đồ thị hàm số $f$ chỉ có thể có tiệm cận ngang khi tập xác định của nó là một khoảng vô hạn hay một nửa khoảng vô hạn (nghĩa là biến $x$ có thể tiến đến $ + \infty $ hoặc $ – \infty $).
+ Đồ thị hàm số $f$ chỉ có thể có tiệm cận đứng khi tập xác định của nó có một trong các dạng sau: $(a;b)$, $[a;b)$, $(a;b]$, $(a;+∞)$, $(-∞;b)$ hoặc là hợp của các tập hợp này và tập xác định không có một trong các dạng sau: $R$, $(c;+∞)$, $(-∞;d)$, $[c;d]$.
2. Tìm tiệm cận xiên của đồ thị hàm số $y = f(x)$
Thực hiện theo các bước sau:
+ Bước 1. Tìm tập xác định của hàm số (đồ thị hàm số $f$ chỉ có thể có tiệm cận xiên nếu tập xác định của nó làlà một khoảng vô hạn hay một nửa khoảng vô hạn).
+ Bước 2. Sử dụng định nghĩa về tiệm cận xiên. Hoặc sử dụng định lí sau:
Nếu $\mathop {\lim }\limits_{x \to + \infty } \frac{{f(x)}}{x} = a \ne 0$ và $\mathop {\lim }\limits_{x \to + \infty } [f(x) – ax] = b$ hoặc $\mathop {\lim }\limits_{x \to – \infty } \frac{{f(x)}}{x} = a \ne 0$ và $\mathop {\lim }\limits_{x \to – \infty } [f(x) – ax] = b$ thì đường thẳng ${\rm{y}} = {\rm{ax}} + {\rm{b}}$ là tiệm cận xiên của đồ thị hàm số $f$.
CHÚ Ý: Đối với hàm phân thức: $f\left( x \right) = \frac{{P(x)}}{{Q(x)}}$ trong đó $P(x)$, $Q(x)$ là hai đa thức của $x$ ta thường dùng phương pháp sau để tìm các đường tiệm cận của đồ thị hàm số:
a. Tiệm cận đứng
+ Nếu $\left\{ \begin{array}{l}
P({x_0}) \ne 0\\
Q({x_0}) = 0
\end{array} \right.$ thì đường thẳng: $x = {x_0}$ là tiệm cận đứng của đồ thị hàm số.
b. Tiệm cận ngang
+ Nếu bậc của $P(x)$ bé hơn bậc của $Q(x)$ thì đồ thị của hàm số có tiệm cận ngang là trục hoành độ.
+ Nếu bậc của $P(x)$ bằng bậc của $Q(x)$ thì đồ thị hàm có tiệm cận ngang là đường thẳng: $y = \frac{A}{B}$ trong đó $A$, $B$ lần lượt là hệ số của số hạng có số mũ lớn nhất của $P(x)$ và $Q(x).$
+ Nếu bậc của $P(x)$ lớn hơn bậc của $Q(x)$ thì đồ thị của hàm số không có tiệm cận ngang.
c. Tiệm cận xiên
+ Nếu bậc của $P(x)$ bé hơn hay bằng bậc của $Q(x)$ hoặc lớn hơn bậc của $Q(x)$ từ hai bậc trở lên thì đồ thị hàm số không có tiệm cận xiên.
+ Nếu bậc của $P(x)$ lớn hơn bậc của $Q(x)$ một bậc và $P(x)$ không chia hết cho $Q(x)$ thì đồ thị hàm có tiệm cận xiên và ta tìm tiệm cận xiên bằng cách chia $P(x)$ cho $Q(x)$ và viết ${\rm{f}}\left( {\rm{x}} \right) = {\rm{ax}} + {\rm{b}} + \frac{{R(x)}}{{Q(x)}}$, trong đó $\mathop {\lim }\limits_{x \to + \infty } \frac{{R(x)}}{{Q(x)}} = 0$, $\mathop {\lim }\limits_{x \to – \infty } \frac{{R(x)}}{{Q(x)}} = 0$. Suy ra đường thẳng ${\rm{y}} = {\rm{ax}} + {\rm{b}}$ là tiệm cận xiên của đồ thị hàm số.
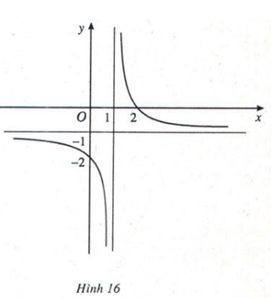
Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 27: Cho hàm số y = (2 – x)/(x – 1) (H.16) có đồ thị (C).
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
Lời giải:
Khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞ dần tiến về 0.
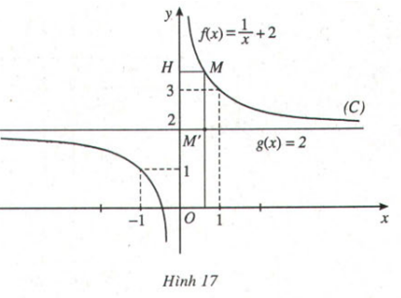
Trả lời câu hỏi Toán 12 Giải tích Bài 4 trang 29: Tính ![]() và nêu nhận xét về khoảng cách MH khi x → 0 (H.17)
và nêu nhận xét về khoảng cách MH khi x → 0 (H.17)
Lời giải:
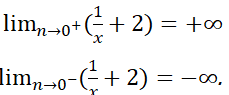
Khi x dần đến 0 thì độ dài đoạn MH cũng dần đến 0.