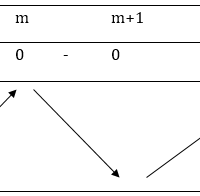
Tìm tham số m để hàm số đơn điệu trên một miền Ta xét dạng toán tìm điều kiện của tham số $m$ để hàm số đơn điệu trên $R$ hoặc trên khoảng con của $R.$ Lý thuyết: Cho hàm số $y = f\left( {x,m} \right)$ với $m$ là tham số xác định trên một khoảng $I.$ a. Hàm số đồng biến trên $I$ $ \Leftrightarrow y’ \ge 0, \forall x \in I$ và $y’ = 0$ chỉ xảy ra tại hữu hạn điểm. b. … [Đọc thêm...] vềTìm tham số m để hàm số đơn điệu trên một miền

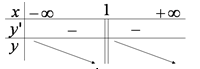
Đồng biến, nghịch biến của hàm số khác Các bước xét tính đơn điệu của hàm số Bước 1 : Tìm tập xác định Bước 2:  Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định. Bước 3:  Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên. Bước 4:  Nêu kết luận về các khoảng đồng biến, nghịch biến … [Đọc thêm...] vềĐồng biến, nghịch biến của hàm số khác

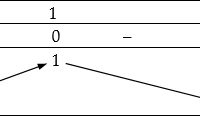
Đồng biến, nghịch biến của hàm số trùng phương Các bước xét tính đơn điệu của hàm số Bước 1 : Tìm tập xác định Bước 2:  Tính đạo hàm \(f'(x)=0\). Tìm các điểm \(x_i\) (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định. Bước 3:  Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên. Bước 4:  Nêu kết luận về các khoảng đồng biến, … [Đọc thêm...] vềĐồng biến, nghịch biến của hàm số trùng phương

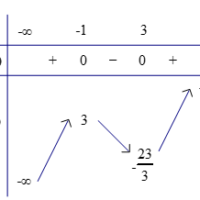
Đồng biến, nghịch biến của hàm số bậc ba, không chứa tham số. VD 1: Tìm khoảng đơn điệu của hàm số $y = {x^3} – 6{x^2} + 9x – 3.$ TXĐ: $D = R.$ Ta có: ${\rm{y’}} = {\rm{3}}{{\rm{x}}^{\rm{2}}}–{\rm{12x}} + {\rm{9}}.$ ${\rm{y’}} = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = 3 \end{array} \right.$ Giới hạn: $\mathop {\lim }\limits_{x \to – \infty } y = – … [Đọc thêm...] vềĐồng biến, nghịch biến của hàm số bậc ba

1. Định nghĩa Kí hiệu: K là một khoảng, một đoạn hoặc một nửa khoảng. Cho hàm số \(y=f(x)\) xác định trên K. Hàm số \(y=f(x)\) đồng biến (tăng) trên K nếu \(\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) < f({x_2})\). Hàm số \(y=f(x)\) nghịch biến (giảm) trên K nếu \(\left\{ … [Đọc thêm...] vềLý thuyết đồng biến, nghịch biến của hàm số