Đề: Cho hình nón có thiết diện qua trục là tam giác vuông vân có cạnh góc vuông bằng 2. Tính diện tích của thiết diện đi qua đỉnh và cắt đáy của hình nón theo cung \({120^0}.\)

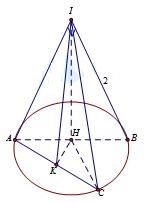
Ta có: \(AB = \sqrt {{2^2} + {2^2}}  = 2\sqrt 2  \Rightarrow AH = HC = \frac{{AB}}{2} = \sqrt 2 \)

\(A{C^2} = A{H^2} + H{C^2} – 2.AH.HC\cos {120^0} = 2{\left( {\sqrt 2 } \right)^2} – 2{\left( {\sqrt 2 } \right)^2}\left( { – \frac{1}{2}} \right) = 6\) \( \Rightarrow AC = \sqrt 6 \).

Gọi K là trung điểm của AC.

Ta có: \(KH = \sqrt {A{H^2} – A{K^2}}  = \sqrt {{{\left( {\sqrt 2 } \right)}^2} – {{\left( {\frac{{\sqrt 6 }}{2}} \right)}^2}}  = \frac{1}{2};IH = \frac{{AB}}{2} = \sqrt 2 \) 

\(IK = \sqrt {I{H^2} + K{H^2}}  = \sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^2}}  = \sqrt {\frac{5}{2}} ;{S_{IAC}} = \frac{1}{2}IK.AC = \frac{1}{2}\sqrt {\frac{6}{2}} .\sqrt 6  = \frac{{\sqrt {15} }}{2}.\)