[4] Trong không gian \(Oxyz\), cho hai điểm \(A\left( {4; - 2;4} \right),B\left( { - 2;6;4} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = 5\\y = - 1\\z = t\end{array} \right..\) Gọi \(M\) là điểm di động thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(\widehat {AMB} = 90^\circ \) và \(N\) là điểm di động luôn cách \(d\) một khoảng là 1 đơn vị và cách mặt phẳng … [Đọc thêm...] về[4] Trong không gian \(Oxyz\), cho hai điểm \(A\left( {4; – 2;4} \right),B\left( { – 2;6;4} \right)\) và đường thẳng \(d:\left\{ \begin{array}{l}x = 5\\y = – 1\\z = t\end{array} \right..\) Gọi \(M\) là điểm di động thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(\widehat {AMB} = 90^\circ \) và \(N\) là điểm di động luôn cách \(d\) một khoảng là 1 đơn vị và cách mặt phẳng \(\left( {Oxy} \right)\) một khoảng không quá 3 đơn vị. Tổng giá trị nhỏ nhất và giá trị lớn nhất của \(MN\) bằng
[4] Trong mặt phẳng toạ độ \(Oxyz\) cho mặt cầu \(\left( S \right)\) có phương trình \(\,{\left( {x – 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 3} \right)^2} = 3\). Xét khối trụ \(\left( T \right)\) có trục song song với trục \(Ox\) và có hai đường tròn đáy nằm trên mặt cầu \(\left( S \right)\). Khi \(\left( T \right)\) có thể tích lớn nhất, giả sử phương trình các mặt phẳng chứa hai đường tròn đáy của \(\left( T \right)\) là \(x + by + cz + d = 0\) và \(x + by + cz + d’ = 0\) \(\left( {d > d’} \right)\). Giá trị của \(2d – d’\) bằng
[4] Trong mặt phẳng toạ độ \(Oxyz\) cho mặt cầu \(\left( S \right)\) có phương trình \(\,{\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 3} \right)^2} = 3\). Xét khối trụ \(\left( T \right)\) có trục song song với trục \(Ox\) và có hai đường tròn đáy nằm trên mặt cầu \(\left( S \right)\). Khi \(\left( T \right)\) có thể tích lớn nhất, giả sử phương trình … [Đọc thêm...] về[4] Trong mặt phẳng toạ độ \(Oxyz\) cho mặt cầu \(\left( S \right)\) có phương trình \(\,{\left( {x – 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z – 3} \right)^2} = 3\). Xét khối trụ \(\left( T \right)\) có trục song song với trục \(Ox\) và có hai đường tròn đáy nằm trên mặt cầu \(\left( S \right)\). Khi \(\left( T \right)\) có thể tích lớn nhất, giả sử phương trình các mặt phẳng chứa hai đường tròn đáy của \(\left( T \right)\) là \(x + by + cz + d = 0\) và \(x + by + cz + d’ = 0\) \(\left( {d > d’} \right)\). Giá trị của \(2d – d’\) bằng
[4] Trong không gian \(Oxyz\) cho hình nón \(\left( N \right)\)có đỉnh \(S\left( {4;5; – 3} \right)\), bán kính đáy \({\rm{12 }}\)và đường tròn đáy nằm trên mặt phẳng \(\left( P \right):x + 2y – 2z + 28 = 0\). Khi cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây?
[4] Trong không gian \(Oxyz\) cho hình nón \(\left( N \right)\)có đỉnh \(S\left( {4;5; - 3} \right)\), bán kính đáy \({\rm{12 }}\)và đường tròn đáy nằm trên mặt phẳng \(\left( P \right):x + 2y - 2z + 28 = 0\). Khi cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây? A. \(170\). B. … [Đọc thêm...] về[4] Trong không gian \(Oxyz\) cho hình nón \(\left( N \right)\)có đỉnh \(S\left( {4;5; – 3} \right)\), bán kính đáy \({\rm{12 }}\)và đường tròn đáy nằm trên mặt phẳng \(\left( P \right):x + 2y – 2z + 28 = 0\). Khi cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây?
[4] Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + y + z = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {0;1;2} \right)\) bán kính \(R = 1\). Xét điểm \(M\) thay đổi trên \(\left( P \right)\). Khối nón \(\left( N \right)\) có đỉnh là \(I\) và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( S \right)\). Khi \(\left( N \right)\) có thể tích lớn nhất, mặt phẳng chứa đường tròn đáy của \(\left( N \right)\) có phương trình là \(x + ay + bz + c = 0\). Giá trị của \(a + b + c\) bằng
[4] Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + y + z = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {0;1;2} \right)\) bán kính \(R = 1\). Xét điểm \(M\) thay đổi trên \(\left( P \right)\). Khối nón \(\left( N \right)\) có đỉnh là \(I\) và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( S \right)\). … [Đọc thêm...] về[4] Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):x + y + z = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {0;1;2} \right)\) bán kính \(R = 1\). Xét điểm \(M\) thay đổi trên \(\left( P \right)\). Khối nón \(\left( N \right)\) có đỉnh là \(I\) và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( S \right)\). Khi \(\left( N \right)\) có thể tích lớn nhất, mặt phẳng chứa đường tròn đáy của \(\left( N \right)\) có phương trình là \(x + ay + bz + c = 0\). Giá trị của \(a + b + c\) bằng
4] Trong không gian \(Oxyz\), cho hai điểm \(A\left( {\frac{{5 + \sqrt 3 }}{2}\,;\,\frac{{7 – \sqrt 3 }}{2}\,;\,3} \right)\,,\,B\left( {\frac{{5 – \sqrt 3 }}{2}\,;\,\frac{{7 + \sqrt 3 }}{2}\,;\,3} \right)\) và mặt cầu \(\left( S \right)\,:{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 6\). Xét mặt phẳng \(\left( P \right):ax + by + cz + d = 0\,\,,\,\)\(\left( {a\,,\,b\,,\,c\,,\,d \in \mathbb{Z}\,:d < – 5} \right)\) là mặt phẳng thay đổi luôn đi qua hai điểm \(A\,,\,B\). Gọi \(\left( N \right)\) là hình nón có đỉnh là tâm của mặt cầu \(\left( S \right)\) và đường tròn đáy là đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\). Tính giá trị của \(T = \left| {a + b + c + d} \right|\) khi thiết diện qua trục của hình nón \(\left( N \right)\) có diện tích lớn nhất.
4] Trong không gian \(Oxyz\), cho hai điểm \(A\left( {\frac{{5 + \sqrt 3 }}{2}\,;\,\frac{{7 - \sqrt 3 }}{2}\,;\,3} \right)\,,\,B\left( {\frac{{5 - \sqrt 3 }}{2}\,;\,\frac{{7 + \sqrt 3 }}{2}\,;\,3} \right)\) và mặt cầu \(\left( S \right)\,:{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 6\). Xét mặt phẳng \(\left( P \right):ax + by + cz + d … [Đọc thêm...] về4] Trong không gian \(Oxyz\), cho hai điểm \(A\left( {\frac{{5 + \sqrt 3 }}{2}\,;\,\frac{{7 – \sqrt 3 }}{2}\,;\,3} \right)\,,\,B\left( {\frac{{5 – \sqrt 3 }}{2}\,;\,\frac{{7 + \sqrt 3 }}{2}\,;\,3} \right)\) và mặt cầu \(\left( S \right)\,:{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 6\). Xét mặt phẳng \(\left( P \right):ax + by + cz + d = 0\,\,,\,\)\(\left( {a\,,\,b\,,\,c\,,\,d \in \mathbb{Z}\,:d < – 5} \right)\) là mặt phẳng thay đổi luôn đi qua hai điểm \(A\,,\,B\). Gọi \(\left( N \right)\) là hình nón có đỉnh là tâm của mặt cầu \(\left( S \right)\) và đường tròn đáy là đường tròn giao tuyến của \(\left( P \right)\) và \(\left( S \right)\). Tính giá trị của \(T = \left| {a + b + c + d} \right|\) khi thiết diện qua trục của hình nón \(\left( N \right)\) có diện tích lớn nhất.
[4] Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;0;0} \right)\), \(B\left( {0;2;0} \right)\) và \(C\left( {0;0;3} \right)\). Mặt cầu \(\left( S \right)\) luôn qua \(A\), \(B\), \(C\) và đồng thời cắt ba tia \(Ox\), \(Oy\), \(Oz\) tại ba điểm phân biệt \(M\), \(N\), \(P\). Gọi \(H\) là trực tâm của tam giác \(MNP\). Tìm giá trị nhỏ nhất của \(HI\) với \(I\left( {4;2;2} \right)\).
[4] Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;0;0} \right)\), \(B\left( {0;2;0} \right)\) và \(C\left( {0;0;3} \right)\). Mặt cầu \(\left( S \right)\) luôn qua \(A\), \(B\), \(C\) và đồng thời cắt ba tia \(Ox\), \(Oy\), \(Oz\) tại ba điểm phân biệt \(M\), \(N\), \(P\). Gọi \(H\) là trực tâm của tam giác \(MNP\). Tìm giá trị nhỏ nhất của \(HI\) với … [Đọc thêm...] về[4] Trong không gian với hệ tọa độ \(Oxyz\), cho ba điểm \(A\left( {1;0;0} \right)\), \(B\left( {0;2;0} \right)\) và \(C\left( {0;0;3} \right)\). Mặt cầu \(\left( S \right)\) luôn qua \(A\), \(B\), \(C\) và đồng thời cắt ba tia \(Ox\), \(Oy\), \(Oz\) tại ba điểm phân biệt \(M\), \(N\), \(P\). Gọi \(H\) là trực tâm của tam giác \(MNP\). Tìm giá trị nhỏ nhất của \(HI\) với \(I\left( {4;2;2} \right)\).
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f’\left( x \right) = \left( {{x^2} – 9} \right)\left( {x – 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} – m} \right)\) có đúng \(7\) điểm cực trị
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 9} \right)\left( {x - 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} - m} \right)\) có đúng \(7\) điểm cực trị A. \(3\) B. \(4\) C. \(5\) D. \(6\) Lời giải: Ta có \(g'\left( x … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f’\left( x \right) = \left( {{x^2} – 9} \right)\left( {x – 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} – m} \right)\) có đúng \(7\) điểm cực trị
[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { – 3} \right) = f\left( {\frac{3}{2}} \right) = – \frac{{19}}{4}\) và đồ thị hàm số \(y = f’\left( x \right)\) có dạng như hình vẽ.
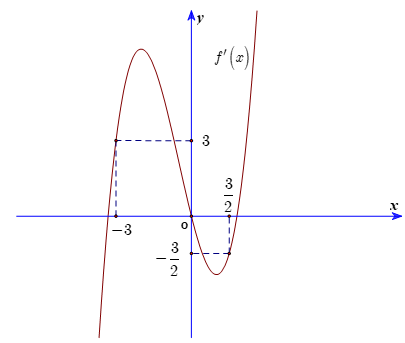
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { – 2;\frac{3}{2}} \right]\) là
[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { - 3} \right) = f\left( {\frac{3}{2}} \right) = - \frac{{19}}{4}\) và đồ thị hàm số \(y = f'\left( x \right)\) có dạng như hình vẽ. Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( … [Đọc thêm...] về[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { – 3} \right) = f\left( {\frac{3}{2}} \right) = – \frac{{19}}{4}\) và đồ thị hàm số \(y = f’\left( x \right)\) có dạng như hình vẽ.
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { – 2;\frac{3}{2}} \right]\) là
[ Mức độ 4 ] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} – 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} – 4x + m} \right)\) có \(5\) điểm cực trị?
[ Mức độ 4 ] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} - 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} - 4x + m} \right)\) có \(5\) điểm cực trị? A.\(8.\) B. \(7.\) C. \(6.\) D. \(5.\) Lời giải: Đặt \(g\left( x … [Đọc thêm...] về[ Mức độ 4 ] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} – 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} – 4x + m} \right)\) có \(5\) điểm cực trị?
[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { – 6} \right) = 42\) và bảng xét dấu đạo hàm như

Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { – \,3{x^4}\,\, + \,\,12{x^2}\, – \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, – 48{x^2}\) trên đoạn \(\left[ { – 1;1} \right]\) bằng
[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { - 6} \right) = 42\) và bảng xét dấu đạo hàm như Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { - \,3{x^4}\,\, + \,\,12{x^2}\, - \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, - 48{x^2}\) trên đoạn \(\left[ { - 1;1} \right]\) bằng A. 3. B. 0. C. 1. D. 2. Lời … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { – 6} \right) = 42\) và bảng xét dấu đạo hàm như
Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { – \,3{x^4}\,\, + \,\,12{x^2}\, – \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, – 48{x^2}\) trên đoạn \(\left[ { – 1;1} \right]\) bằng
