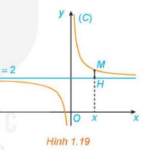
Giải chi tiết Giải SGK Toán 12 (Sách KNTT) Bài 3: Đường tiệm cận của đồ thị hàm số - SÁCH GIÁO KHOA TOÁN 12 KẾT NỐI - 2024 ================ Giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số 1. Đường tiệm cận ngang HĐ1 trang 20 Toán 12 Tập 1: Cho hàm số y=f(x)=2x+1x có đồ thị (C). Với x>0, xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên … [Đọc thêm...] vềGiải SGK Toán 12 (Sách KNTT) Bài 3: Đường tiệm cận của đồ thị hàm số
Giải SGK Toán 12 (Sách KNTT) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giải chi tiết Giải SGK Toán 12 (Sách KNTT) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - SÁCH GIÁO KHOA TOÁN 12 KẾT NỐI - 2024 ================ Bài 1.10: Đề bài Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) \(y = - {x^2} + 4x + 3\); b) \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\); c) \(y = \frac{{{x^2} - 2x + 3}}{{x … [Đọc thêm...] vềGiải SGK Toán 12 (Sách KNTT) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giải SGK Toán 12 (Sách KNTT) Bài 1: Tính đơn điệu và cực trị của hàm số
Giải chi tiết Giải SGK Toán 12 (Sách KNTT) Bài 1: Tính đơn điệu và cực trị của hàm số - SÁCH GIÁO KHOA TOÁN 12 KẾT NỐI - 2024 ================ HĐ1 Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 12 Kết nối tri thức Quan sát đồ thị của hàm số \(y = {x^2}\) (H.1.2) a) Hàm số đồng biến trên khoảng nào? b) Hàm số nghịch biến trên khoảng nào? Phương pháp giải: Sử dụng kiến … [Đọc thêm...] vềGiải SGK Toán 12 (Sách KNTT) Bài 1: Tính đơn điệu và cực trị của hàm số
Đề thi thử TN THPT Toán 2024 – SƠN LA – LẦN 2 -.docx
Đề thi thử TN THPT Toán 2024 – SƠN LA - LẦN 2 -.docx ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên internet.... ———– xem file de thi … [Đọc thêm...] vềĐề thi thử TN THPT Toán 2024 – SƠN LA – LẦN 2 -.docx
Đề thi thử TN THPT Toán 2024 – CHUYÊN HẠ LONG LẦN 3 -.pdf
Đề thi thử TN THPT Toán 2024 – CHUYÊN HẠ LONG LẦN 3 -.pdf ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên internet.... ———– xem file de thi … [Đọc thêm...] vềĐề thi thử TN THPT Toán 2024 – CHUYÊN HẠ LONG LẦN 3 -.pdf
SÁCH GIÁO KHOA Toán lớp 9 – 2024
SÁCH GIÁO KHOA Toán lớp 9 – 2024 Sách giáo khoa toán - KẾT NỐI TRI THỨC Sách giáo khoa toán - CHÂN TRỜI SÁNG TẠO Sách giáo khoa toán - CÁNH DIỀU Sách giáo khoa toán - CÙNG KHÁM PHÁ SGK TOÁN 9 CKP TẬP 1.pdf SGK TOÁN 9 CKP TẬP 2.pdf … [Đọc thêm...] vềSÁCH GIÁO KHOA Toán lớp 9 – 2024
[4] Trong không gian với hệ trục tọa độ \(Oxyz\) cho mặt phẳng \(\left( P \right):2x – y – 2z – 2 = 0\) và mặt phẳng \(\left( Q \right):2x – y – 2z + 10 = 0\) song song với nhau. Biết \(A\;(1\,;\,2\,;\,1)\) là điểm nằm giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(\left( S \right)\) là mặt cầu qua \(A\) và tiếp xúc với cả hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Biết rằng khi \(\left( S \right)\) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính \(r\) của đường tròn đó
[4] Trong không gian với hệ trục tọa độ \(Oxyz\) cho mặt phẳng \(\left( P \right):2x - y - 2z - 2 = 0\) và mặt phẳng \(\left( Q \right):2x - y - 2z + 10 = 0\) song song với nhau. Biết \(A\;(1\,;\,2\,;\,1)\) là điểm nằm giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(\left( S \right)\) là mặt cầu qua \(A\) và tiếp xúc với cả hai mặt phẳng \(\left( P … [Đọc thêm...] về[4] Trong không gian với hệ trục tọa độ \(Oxyz\) cho mặt phẳng \(\left( P \right):2x – y – 2z – 2 = 0\) và mặt phẳng \(\left( Q \right):2x – y – 2z + 10 = 0\) song song với nhau. Biết \(A\;(1\,;\,2\,;\,1)\) là điểm nằm giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(\left( S \right)\) là mặt cầu qua \(A\) và tiếp xúc với cả hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\). Biết rằng khi \(\left( S \right)\) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính \(r\) của đường tròn đó
[4] Trong không gian \(Oxyz,\) cho điểm \(A\left( {2\,; – \,1\,; – 3} \right)\)và mặt cầu \(\left( S \right)\) có phương trình: \(\,{\left( {x – 4} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 4} \right)^2} = 25.\) Gọi \(\left( C \right)\) là giao tuyến của \(\left( S \right)\)với mặt phẳng \(\left( {Oyz} \right).\) Lấy hai điểm \(M,\,N\)trên \(\left( C \right)\) sao cho \(MN = 2\sqrt 5 .\) Khi tứ diện \(OAMN\)có thể tích lớn nhất thì đường thẳng \(MN\)đi qua điểm nào trong số các điểm dưới đây?
[4] Trong không gian \(Oxyz,\) cho điểm \(A\left( {2\,; - \,1\,; - 3} \right)\)và mặt cầu \(\left( S \right)\) có phương trình: \(\,{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 4} \right)^2} = 25.\) Gọi \(\left( C \right)\) là giao tuyến của \(\left( S \right)\)với mặt phẳng \(\left( {Oyz} \right).\) Lấy hai điểm \(M,\,N\)trên \(\left( C \right)\) sao … [Đọc thêm...] về[4] Trong không gian \(Oxyz,\) cho điểm \(A\left( {2\,; – \,1\,; – 3} \right)\)và mặt cầu \(\left( S \right)\) có phương trình: \(\,{\left( {x – 4} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 4} \right)^2} = 25.\) Gọi \(\left( C \right)\) là giao tuyến của \(\left( S \right)\)với mặt phẳng \(\left( {Oyz} \right).\) Lấy hai điểm \(M,\,N\)trên \(\left( C \right)\) sao cho \(MN = 2\sqrt 5 .\) Khi tứ diện \(OAMN\)có thể tích lớn nhất thì đường thẳng \(MN\)đi qua điểm nào trong số các điểm dưới đây?
[4] Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( {0;1;2} \right)\), mặt phẳng \(\left( \alpha \right)\): \(x + y – z + 4 = 0\) và mặt cầu \(\left( S \right):{\left( {x – 3} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 2} \right)^2} = 25\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A,\) vuông góc với \(\left( \alpha \right)\) và đồng thời \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Diện tích của hình tròn giao tuyến khi đó là
[4] Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( {0;1;2} \right)\), mặt phẳng \(\left( \alpha \right)\): \(x + y - z + 4 = 0\) và mặt cầu \(\left( S \right):{\left( {x - 3} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 2} \right)^2} = 25\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A,\) vuông góc với \(\left( \alpha \right)\) và đồng thời \(\left( … [Đọc thêm...] về[4] Trong không gian với hệ tọa độ \(Oxyz,\) cho điểm \(A\left( {0;1;2} \right)\), mặt phẳng \(\left( \alpha \right)\): \(x + y – z + 4 = 0\) và mặt cầu \(\left( S \right):{\left( {x – 3} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 2} \right)^2} = 25\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A,\) vuông góc với \(\left( \alpha \right)\) và đồng thời \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Diện tích của hình tròn giao tuyến khi đó là
[4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( {{S_1}} \right)\) có tâm \(I\left( {2;1;1} \right)\) có bán kính bằng 4 và mặt cầu \(\left( {{S_2}} \right)\) có tâm \(J\left( {2;1;5} \right)\) có bán kính \(2\). \(\left( P \right)\) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\). Đặt \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm \(O\) đến \(\left( P \right)\). Giá trị \(M + m\) bằng
[4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( {{S_1}} \right)\) có tâm \(I\left( {2;1;1} \right)\) có bán kính bằng 4 và mặt cầu \(\left( {{S_2}} \right)\) có tâm \(J\left( {2;1;5} \right)\) có bán kính \(2\). \(\left( P \right)\) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\). Đặt \(M,m\) lần lượt là giá trị lớn nhất, giá … [Đọc thêm...] về[4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( {{S_1}} \right)\) có tâm \(I\left( {2;1;1} \right)\) có bán kính bằng 4 và mặt cầu \(\left( {{S_2}} \right)\) có tâm \(J\left( {2;1;5} \right)\) có bán kính \(2\). \(\left( P \right)\) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\). Đặt \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của khoảng cách từ điểm \(O\) đến \(\left( P \right)\). Giá trị \(M + m\) bằng