[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} + x - 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2} - 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} + x – 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} – 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của \(S\).
[Mức độ 3] Cho hàm số \(f(x) = {x^5} + 3{x^3} – 4\;m\). Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f(x) + m}}} \right) = {x^3} – m\) có nghiệm thuộc \(\left[ {1;2} \right]\)?
[Mức độ 3] Cho hàm số \(f(x) = {x^5} + 3{x^3} - 4\;m\). Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f(x) + m}}} \right) = {x^3} - m\) có nghiệm thuộc \(\left[ {1;2} \right]\)? A. \(15\). B. \(16\). C. \(17\). D. \(18\). Lời giải: Đặt \({\rm{ }}\sqrt[3]{{f(x) + m}} = u \Rightarrow f(x) + m = {u^3} \Rightarrow \left\{ … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(f(x) = {x^5} + 3{x^3} – 4\;m\). Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt[3]{{f(x) + m}}} \right) = {x^3} – m\) có nghiệm thuộc \(\left[ {1;2} \right]\)?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 5x – 6\,,\,\forall x \in \mathbb{R}\). Tính tổng tất cả các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { – {x^3} + 3x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0\,;\,3} \right)\).
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} - 5x - 6\,,\,\forall x \in \mathbb{R}\). Tính tổng tất cả các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { - {x^3} + 3x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0\,;\,3} \right)\). A. \(119\) . B. \(120\) … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 5x – 6\,,\,\forall x \in \mathbb{R}\). Tính tổng tất cả các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { – {x^3} + 3x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0\,;\,3} \right)\).
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
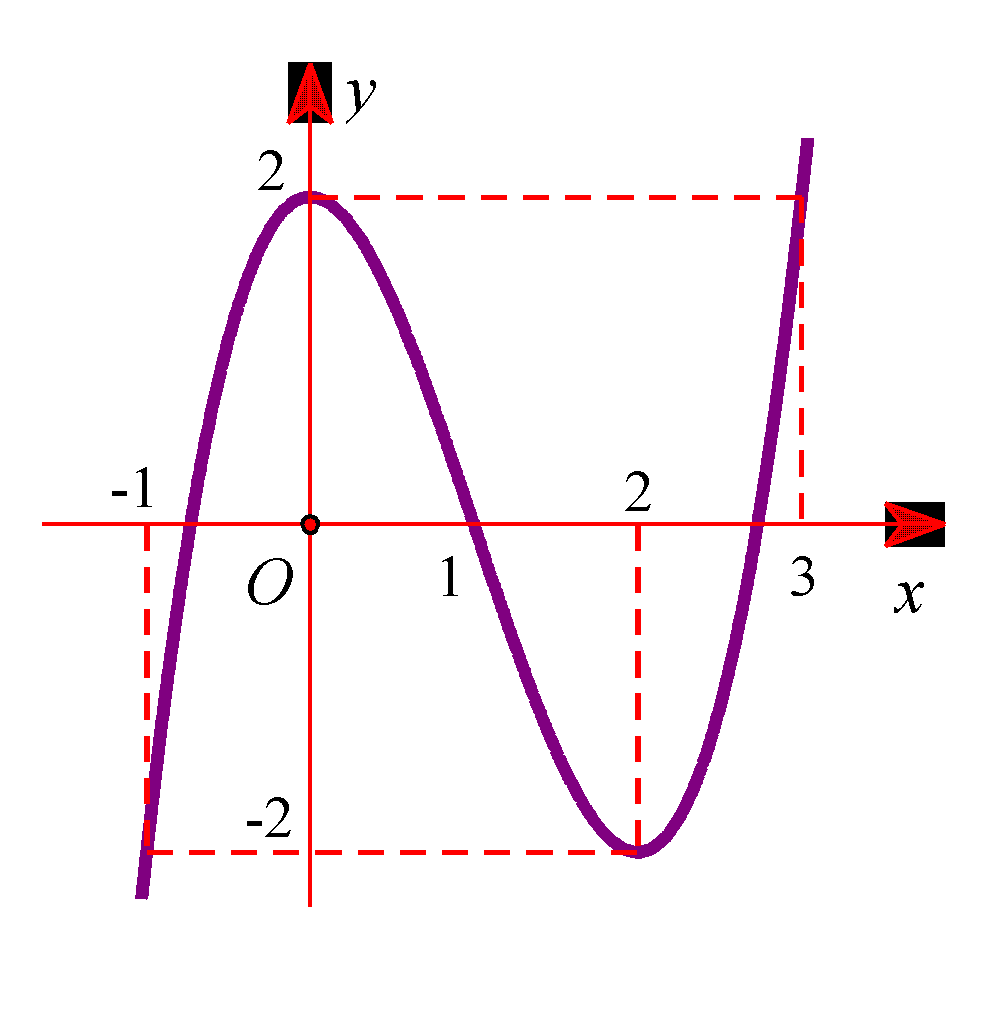
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{\left( {x - m - 1} \right)^2} + 2022\), với \(m\) là tham số thự C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} – 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} – 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
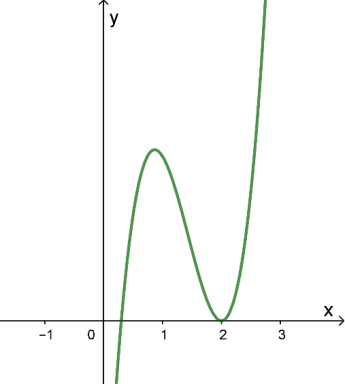
[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} - 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng? A. 4. B. 3. C. 2. D. 6. Lời giải: Quan sát đồ thị hàm số … [Đọc thêm...] về[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} – 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} – 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
[ Mức độ 3] Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
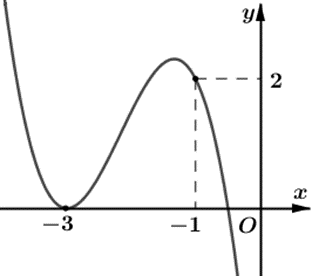
Hỏi đồ thị hàm số \(y = \frac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{x\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]}}\) có bao nhiêu đường tiệm cận đứng?
[ Mức độ 3] Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Hỏi đồ thị hàm số \(y = \frac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{x\left[ {{f^2}\left( x \right) - 2f\left( x \right)} \right]}}\) có bao nhiêu đường tiệm cận đứng? A. \(2\). B. \(3\). C. \(4\). D. \(6\). Lời giải: Điều kiện: \({x^2} + x \ge 0 … [Đọc thêm...] về[ Mức độ 3] Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
Hỏi đồ thị hàm số \(y = \frac{{\left( {{x^2} + 4x + 3} \right)\sqrt {{x^2} + x} }}{{x\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]}}\) có bao nhiêu đường tiệm cận đứng?
[ Mức độ 4] Cho hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) có đạo hàm trên \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\)và \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\). Đồ thị hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) như hình bên. Có bao nhiêu số nguyên dương \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) để hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) nghịch biến trên \(12\)?

[ Mức độ 4] Cho hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\) có đạo hàm trên \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\)và \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\). Đồ thị hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\) như hình bên. Có bao … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) có đạo hàm trên \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\)và \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\). Đồ thị hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) như hình bên. Có bao nhiêu số nguyên dương \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) để hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) nghịch biến trên \(12\)?
[Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ
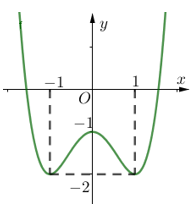
Có bao nhiêu giá trị nguyên của \(m \in \left[ { – 2023;2024} \right]\) sao cho phương trình \(f\left( {\frac{1}{{\ln x – 2}}} \right) = m\) có đúng hai nghiệm.
[Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ Có bao nhiêu giá trị nguyên của \(m \in \left[ { - 2023;2024} \right]\) sao cho phương trình \(f\left( {\frac{1}{{\ln x - 2}}} \right) = m\) có đúng hai nghiệm. A. \(2027\). B. \(2026\). C. \(2025\). D.\(2024\). Lời giải: Xét \(u\left( x \right) = … [Đọc thêm...] về[Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị như hình vẽ
Có bao nhiêu giá trị nguyên của \(m \in \left[ { – 2023;2024} \right]\) sao cho phương trình \(f\left( {\frac{1}{{\ln x – 2}}} \right) = m\) có đúng hai nghiệm.
[ Mức độ 4] Cho hàm số \(y = {x^3} – 3{x^2} + 2\). Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {{x^4} – 8{x^2}} \right| + m} \right) – 2 = 0\) có đúng 12 nghiệm.
[ Mức độ 4] Cho hàm số \(y = {x^3} - 3{x^2} + 2\). Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {{x^4} - 8{x^2}} \right| + m} \right) - 2 = 0\) có đúng 12 nghiệm. A. 9. B. 10. C. 11. D. 12. Lời giải: Xét phương trình \(y = {x^3} - 3{x^2} + 2 = 2 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = {x^3} – 3{x^2} + 2\). Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\left| {{x^4} – 8{x^2}} \right| + m} \right) – 2 = 0\) có đúng 12 nghiệm.
[Mức độ 4] Xét các số thực thỏa mãn \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} – 2x + 2} \right){.4^x}\). Giá trị lớn nhất của biểu thức \(P = 2{x^2} + {y^2} + 2x – 3\) bằng
[Mức độ 4] Xét các số thực thỏa mãn \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} - 2x + 2} \right){.4^x}\). Giá trị lớn nhất của biểu thức \(P = 2{x^2} + {y^2} + 2x - 3\) bằng A. \(7\). B. \(10\). C. \(9\). D. \(\frac{{17}}{2}\). Lời giải: - Ta có: \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} - 2x + 2} \right){.4^x} \Leftrightarrow {2^{{x^2} + … [Đọc thêm...] về[Mức độ 4] Xét các số thực thỏa mãn \({2^{{x^2} + {y^2} + 1}} \le \left( {{x^2} + {y^2} – 2x + 2} \right){.4^x}\). Giá trị lớn nhất của biểu thức \(P = 2{x^2} + {y^2} + 2x – 3\) bằng
