Bài toán: Một phần sân trường được định vị bởi các điểm $A,B,C,D$ như hình vẽ.
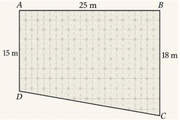
Bước đầu chúng được lấy “thăng bằng” để có cùng độ cao so với mặt đất, biết $ABCD$ là hình thang vuông ở $A$ và $B$ với độ dài $AB=25\mathrm{\,\;m},AD=15\mathrm{\,\;m},BC=18\mathrm{\,\;m}$. Do yêu cầu kĩ thuật, khi lát phẳng phần sân trường phải thoát nước về góc sân ở $C$ nên người ta lấy độ cao ở các điểm $B,C,D$ lần lượt xuống thấp hơn so với độ cao ở $A$ là $10\mathrm{\,\;cm},a\mathrm{\,\;cm},6\mathrm{\,\;cm}$ tương ứng sao cho bốn điểm $A,B’,C’,D’$ đồng phẳng. Tìm giá trị của $a$.
Lòi giải
Đáp án: 17,2.
Đổi: $25\mathrm{\,\;m}=2500\mathrm{\,\;cm};15\mathrm{\,\;m}=1500\mathrm{\,\;cm};18\mathrm{\,\;m}=1800\mathrm{\,\;cm}$.
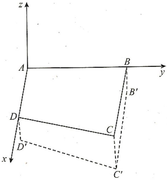
Chọn hệ trục toạ độ $Oxyz$ sao cho: $O$ trùng $A$, tia $Ox$ trùng $AD$; tia $Oy$ trùng $AB$.
Khi đó: $A\left(0;0;0\right),B\left(0;2500;0\right),C\left(1800;2500;0\right),D\left(1500;0;0\right)$.
Khi hạ độ cao các điểm ở các điểm $B,C,D$ lần lượt xuống thấp hơn so với độ cao ở $A$ là: $10\mathrm{\,\;cm},a\mathrm{\,\;cm},6\mathrm{\,\;cm}$ tương ứng thì ta có các điểm mới: $B’\left(0;2500;-10\right),C’\left(1800;2500;-a\right),D’\left(1500;0;-6\right)$.
Theo bài ra có bốn điểm $A,B’,C’,D’$ đồng phẳng.
Vectơ pháp tuyến của mặt phẳng $\left(AB’D’\right)$ là $\vec n=\left[\overrightarrow {AB’} ,\overrightarrow {AD’} \right]=\left(1;1;250\right)$.
Phương trình mặt phẳng $\left(AB’D’\right)$ là: $x+y+250z=0$.
Vì $C’\left(1800;2500;-a\right)\in \left(AB’D’\right)$ nên ta có: $1800+2500-250a=0\Leftrightarrow a=17,2$. Vậy $a=17,2$.
