Trong không gian $Oxyz$, cho véc-tơ $\overrightarrow{a}=(1;-1;0)$ và hai điểm $A(-4;7;3)$, $B(4;4;5)$

Trong không gian $Oxyz$, cho véc-tơ $\overrightarrow{a}=(1;-1;0)$ và hai điểm $A(-4;7;3)$, $B(4;4;5)$. Hai điểm $M$, $N$ thay đổi thuộc mặt phẳng $(Oxy)$ sao cho $\overrightarrow{MN}$ cùng hướng với $\overrightarrow{a}$ và $MN=5\sqrt{2}$. Giá trị lớn nhất của $\left| AM-BN \right|$ bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Đáp án: 4,12
Lời giải: Vì $\overrightarrow{MN}$ cùng hướng với $\overrightarrow{a}$ nên tồn tại số thực $k{>}0$ sao cho $\overrightarrow{MN}=k\overrightarrow{a}\Leftrightarrow MN=\left| k \right|\cdot\left| \overrightarrow{a} \right|\Leftrightarrow \left| k \right|=5\Leftrightarrow k=5.$
Gọi $K\left( x;y;z \right)$ thỏa mãn
$\overrightarrow{AK}=\overrightarrow{MN}$, ta có
$\left\{\begin{array}{l} x+4=5 \\ y-7=-5 \\ z-3=0\end{array}\right. \Leftrightarrow \left\{\begin{array}{l} x=1 \\ y=2 \\ z=3\end{array}\right. \Rightarrow K\left( 1;2;3 \right).$

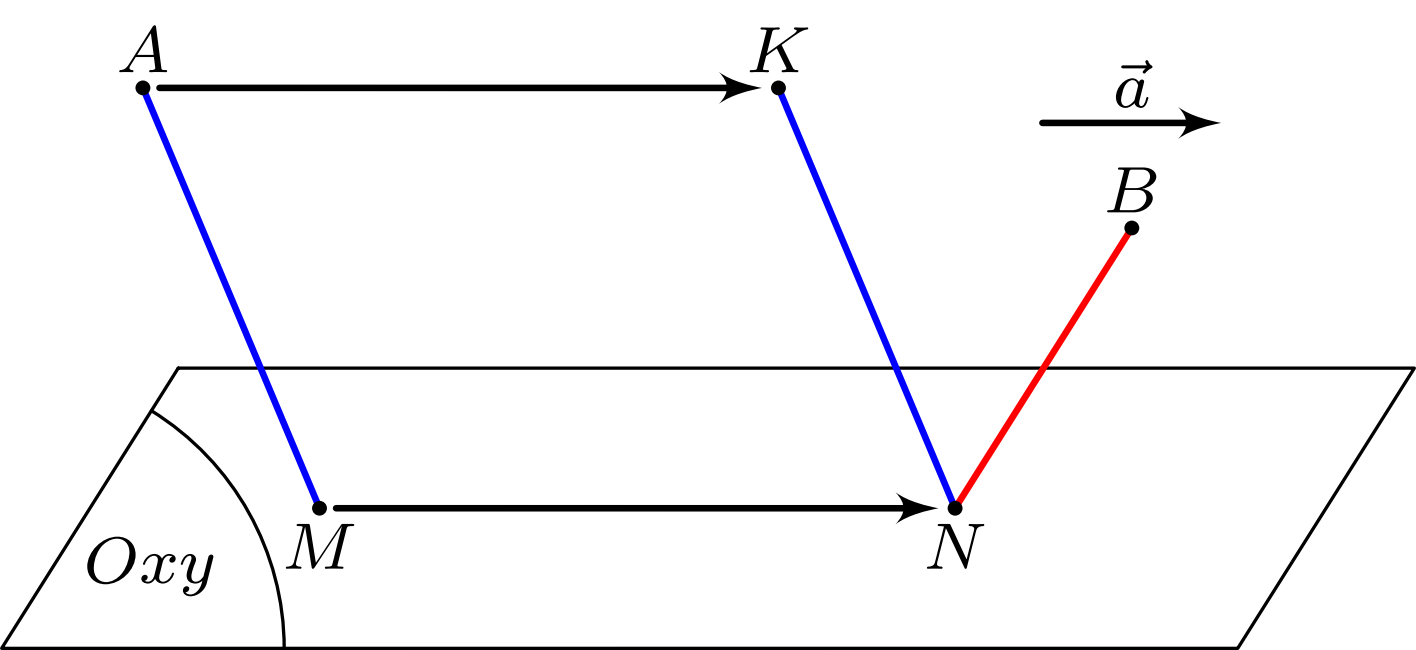
Suy ra $K$ và $B$ nằm cùng phía đối với $\left( Oxy \right)$ và $AM=KN$ (do $AKNM$ là hình bình hành). Khi đó
$\left| AM-BN \right|=\left| KN-BN \right|\le KB=\sqrt{17}.$
Dấu ”$=$”\ xảy ra $\Leftrightarrow K$, $N$, $B$ thẳng hàng.
Vậy giá trị lớn nhất của $\left| AM-BN \right|$ bằng $\sqrt{17}\approx 4{,}12$.