Trong không gian với hệ trục tọa độ $Oxyz$ (mỗi đơn vị trên trục tọa độ dài 1cm) được đặt một góc trong một căn phòng. Có một cây quạt trần có ba cánh quạt và mỗi cánh cách đều nhau (minh họa như hình vẽ bên). Gọi $A\left( -10;-15;300 \right)$ và $B\left( 12;20;300 \right)$ là hai trong ba đỉnh của cánh quạt trần. Chiều cao của ống treo với hộp điện cánh quạt gắn vào trần nhà là $50$ cm và đỉnh $S\left( a;b;c \right)$ với $a{>}0$ là giao điểm giữa trần nhà và ống treo cánh quạt. Tính $T=a-b+c$. (Kết quả làm tròn đến hàng đơn vị)

Đáp án: 365
Lời giải:
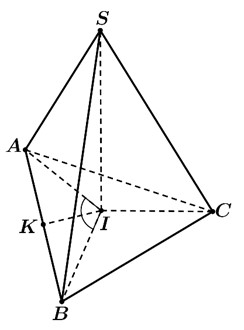
So $SI\bot \left( ABC \right)$ nên ${{z}_{S}}=300+50=350$ nên $S\left( a;b;350 \right)$ và $I\left( a;b;300 \right)$
Do ba cánh quạt cùng năm trên một mặt phẳng $z=300$ nên ta chỉ xét các yếu tố trên cùng mặt phẳng tọa độ (bỏ qua yếu tố cao độ)
Gọi $K$ là trung điểm của $AB$ thì $K\left( 1;\dfrac{5}{2} \right)$ và $\overrightarrow{AB}=\left( 22;35 \right)$
Vectơ $\overrightarrow{KI}\parallel \left( 35;-22 \right)$ nên $\overrightarrow{KI}=k\left( 35;-22 \right)$ mà $KI=AK.\cot 60{}^\circ =\dfrac{AK}{\sqrt{3}}=\sqrt{\dfrac{1709}{12}}$
Do vậy $\left| k\left( 35;-22 \right) \right|=\sqrt{\dfrac{1709}{12}}\Leftrightarrow \left| k \right|=\dfrac{\sqrt{\dfrac{1709}{12}}}{\sqrt{{{35}^{2}}+{{\left( -22 \right)}^{2}}}}=\dfrac{1}{\sqrt{12}}\Rightarrow k=\pm \dfrac{1}{\sqrt{12}}$
Ta có $\left\{ \begin{array}{l} {{x}_{I}}=a={{x}_{K}}+35k \\ {{y}_{I}}=b={{y}_{K}}-22k \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} a=1+35k \\ b=2-22k \end{array} \right.$ mà do $a{>}0\Leftrightarrow 1+35k{>}0\Leftrightarrow k{>}-\dfrac{1}{35}\Rightarrow k=\dfrac{1}{\sqrt{12}}$
Từ đó $\left\{ \begin{array}{l} a=1+35k \\ b=2-22k \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} a=1+\dfrac{35}{\sqrt{12}} \\ b=2-\dfrac{22}{\sqrt{12}} \\ c=350 \end{array} \right.$ nên $T=a-b+c=\left( 1+\dfrac{35}{\sqrt{12}} \right)-\left( 2-\dfrac{22}{\sqrt{12}} \right)+350\approx 365$.
