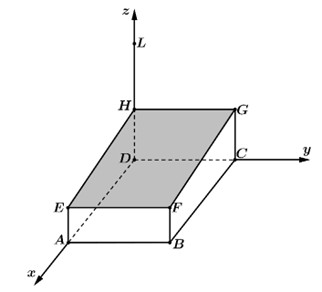
Sân hiên hình chữ nhật của một ngôi nhà là khoảng đất $ABCD$ được lợp mái bằng kính màu để hạn chế ánh sáng đi qua với mái dốc. Các bề mặt bên $ADHE$ và $CGHD$ nằm ở bức tường bên ngoài ngôi nhà. Đặt vào mô hình hệ trục tọa độ như hình vẽ thì ta có $B\left( 5;\dfrac{7}{2};0 \right);E\left( 5;0;2 \right)$ và $H\left( 0;0;3 \right)$. Trên tường nhà có một ngọn đèn đặt tại điểm $L$ cách điểm $D$ một khoảng $6$ m theo phương thẳng đứng. Phần có mái của sân hiên in bóng lên khu vườn bằng phẳng phía trước ngôi nhà dưới ánh đèn tạo thành khoảng đất hạn chế ánh sáng. Tính diện tích khoảng đất đó ( Kết quả làm tròn kết quả đến hàng phần chục).
Đáp án: 45,9
Lời giải:
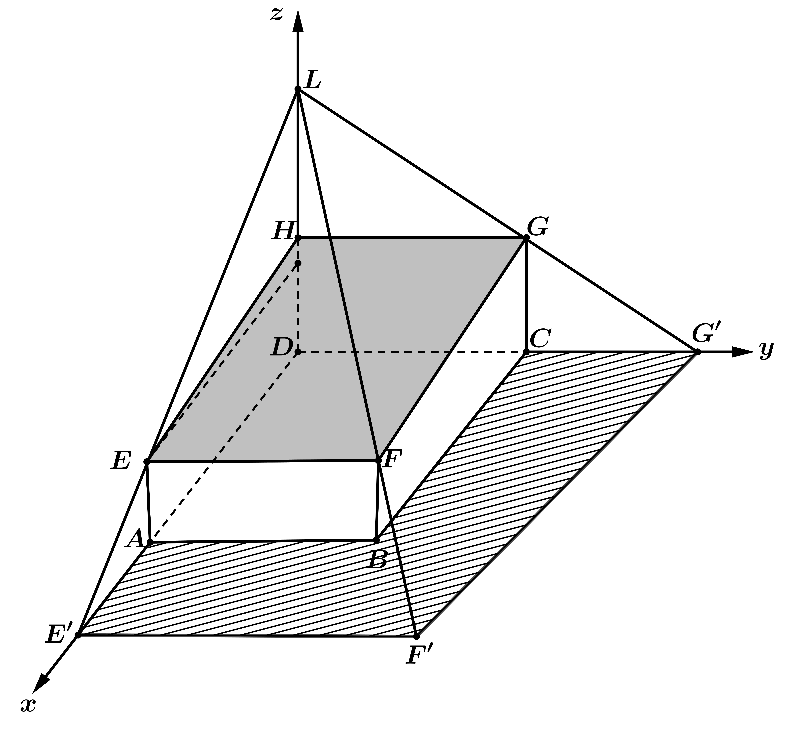
Ta có $H$ là trung điểm của $DL$ nên $GH$ là đường trung bình của $\Delta LD{G}’$ nên ta suy ra $G$ là trung điểm của $L{G}’$. Mặt khác: $GC$ là đường trung bình của $\Delta LD{G}’$ nên ${G}’\left( 0;7;0 \right)$ Ta có: $\dfrac{{E}’A}{ED}=\dfrac{EA}{LD}=\dfrac{2}{6}=\dfrac{1}{3}\Rightarrow {E}’A=\dfrac{1}{3}{E}’D\Rightarrow {E}’A=\dfrac{1}{2}AD=2,5\Rightarrow {E}’\left( 7,5;0 ;0 \right)$ Mặt khác: $\dfrac{EF}{{E}'{F}’}=\dfrac{LE}{L{E}’}=\dfrac{2}{3}\Rightarrow {E}'{F}’=1,5.EF=1,5.3,5=5,25$ Diện tích khoảng đất khi đó là: ${{S}_{D{G}'{F}'{E}’}}=\dfrac{\left( D{G}’+{E}'{F}’ \right).D{E}’}{2}=\dfrac{\left( 7+5,25 \right).7,5}{2}=45,9$
