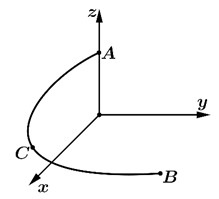
Trượt nước là một trong những trò chơi vận động được nhiều người yêu, thích trong các công viên nước. Một cái máng trượt nước có thiết kế dạng cung tròn với hai đầu mút $A$ và $B$. Chọn hệ trục tọa độ $Oxyz$ với gốc $O$ đặt tại hình chiếu của $A$ trên mặt đất, mặt phẳng $\left( Oxy \right)$ trùng với mặt đất và trục $Oz$ hướng thẳng đứng lên trời, đơn vị đo lấy theo mét (tham khảo hình vẽ dưới đây). Biết tọa độ các điểm các điểm $A\left( 0;0;5 \right),B\left( 6;7;1 \right)$ và một điểm $C\left( 5;0;2 \right)$ nằm trên máng trượt. Độ dài máng trượt nước đó bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)?

Đáp án: 14
Lời giải: Cung tròn $\overset\frown{AB}$ là một phần của đường tròn tâm $I$ và bán kính $IA$
Tam giác $ABC$ nội tiếp đường tròn tâm $I$ và bán kính $IA$
Theo giả thiết: $\left\{ \begin{array}{l} \overrightarrow{AB}=\left( 6;7;-4 \right) \\ \overrightarrow{CA}=\left( -5;0;3 \right) \\ \overrightarrow{CB}=\left( 1;7;-1 \right) \end{array} \right.\Rightarrow \left\{ \begin{array}{l} AB=\sqrt{101} \\ CA=\sqrt{34} \\ CB=\sqrt{51} \end{array} \right.$ nên ${{S}_{ABC}}=\dfrac{AB.CA.CB}{4R}\Rightarrow R=\dfrac{AB.CA.CB}{4{{S}_{ABC}}}$
Dùng công thức Herong: $S=\sqrt{p\left( p-AB \right)\left( p-CA \right)\left( p-CB \right)}$ với $p=\dfrac{AB+CA+CB}{2}$
Vậy bán kính đường tròn ngoại tiếp $\Delta ABC$ là: $R=5,120318806$
Mặt khác: $\cos \widehat{ACB}=\dfrac{\overrightarrow{CA}.\overrightarrow{CB}}{CA.CB}=\dfrac{-5-3}{\sqrt{34}.\sqrt{51}}=-\dfrac{4\sqrt{6}}{51}\Rightarrow \widehat{ACB}=\arccos \left( -\dfrac{4\sqrt{6}}{51} \right)$ (rad)
Suy ra $\widehat{AIB}=2\pi -\arccos \left( -\dfrac{4\sqrt{6}}{51} \right)$ nên ${{l}_{\overset\frown{AB}}}=\widehat{AIB}.R=\left[ 2\pi -\arccos \left( -\dfrac{4\sqrt{6}}{51} \right) \right].R\approx 14$ (m)
