Trong một trò chơi điện tử, nhân vật chính phải xuất phát từ vị trí $A$ để nhặt vật phẩm ở vị trí $M$ di động trên mặt đất và trở lại vị trí $B$. Chọn hệ trục tọa độ $Oxyz$ sao cho $A\left( 1;1;2 \right)$, $B\left( 2;3;4 \right)$ và mặt đất trùng với mặt phẳng $\left( Oxy \right)$. Gọi ${{M}_{0}}\left( a;b;c \right)$ là tọa độ của vật phẩm sao cho quãng đường di chuyển của nhân vật chính là ngắn nhất. Tính tổng $T=a+b+c$.
Đáp án: 3
Lời giải:
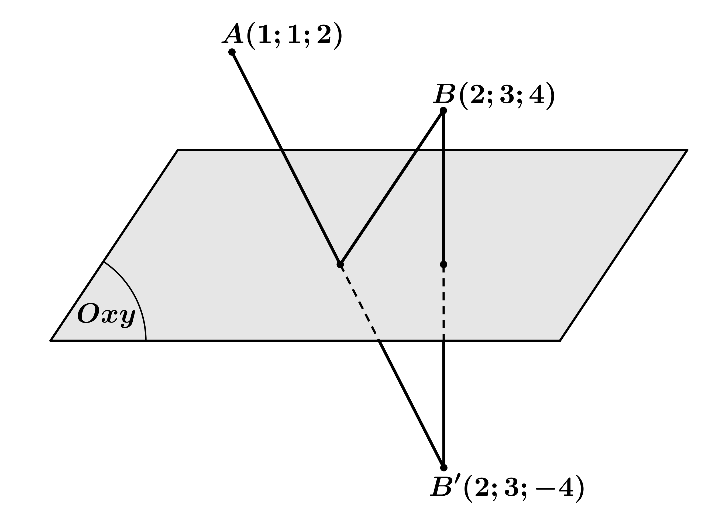
Gọi $S$ là quãng đường mà nhân vật chính phải di chuyển và ${B}’\left( 2;3;-4 \right)$ là điểm đối xứng của $B\left( 2;3;4 \right)$ qua mặt phẳng $\left( Oxy \right)$
Ta có $S=MA+MB=MA+M{B}’\ge A{B}’=\sqrt{{{\left( 2-1 \right)}^{2}}+{{\left( 3-1 \right)}^{2}}+{{\left( -4-2 \right)}^{2}}}=\sqrt{41}$
Dấu bằng xảy ra khi $M\equiv {{M}_{0}}$ là giao điểm của $A{B}’$ và mặt phẳng $\left( Oxy \right)$
Vì ${{M}_{0}}\in \left( Oxy \right)$ nên ${{M}_{0}}\left( a;b;0 \right)$
Mặt khác ba điểm $A,{{M}_{0}},{B}’$ thẳng hàng nên $\overrightarrow{A{{M}_{0}}}$ cùng phương $\overrightarrow{A{B}’}$ với $\overrightarrow{A{{M}_{0}}}=\left( a-1;b-1;-2 \right)$ và $\overrightarrow{A{B}’}=\left( 1;2;-6 \right)$ $\Leftrightarrow \dfrac{a-1}{1}=\dfrac{b-1}{2}=\dfrac{-2}{-6}\Leftrightarrow \left\{ \begin{array}{l} a=\dfrac{4}{3} \\ b=\dfrac{5}{3} \end{array} \right.$. Vậy ${{M}_{0}}\left( \dfrac{4}{3};\dfrac{5}{3};0 \right)$ nên $T=\dfrac{4}{3}+\dfrac{5}{3}+0=3$.
