Một Hai quả bóng bay được thả lên cùng một địa điểm. Sau một khoảng thời gian, quả bóng thứ nhất nằm cách địa điểm xuất phát 200m về hướng Đông và 200m về hướng Nam, đồng thời cách mặt đất 50m; quả bóng thứ hai nằm cách địa điểm xuất phát 100m về hướng Tây và 100m về hướng Bắc, đồng thời cách mặt đất 40m. Cùng thời điểm đó, một người đứng trên mặt đất quan sát thấy hai quả bóng này. Biết rằng so với các vị trí quan sát trên mặt đất, vị trí người đứng có tổng khoảng cách đến hai quả bóng bay là nhỏ nhất. Tính khoảng cách từ vị trí người quan sát đến địa điểm thả hai quả bóng bay này (Đơn vị: mét) (Kết quả làm tròn đến hàng đơn vị).
Đáp án: 47
Lời giải:
Tọa độ của quả bóng bay thứ nhất và thứ hai lần lượt là: $A\left(-200;200;50\right)$ và $B\left(-100;100;40\right)$
Minh họa như sau:
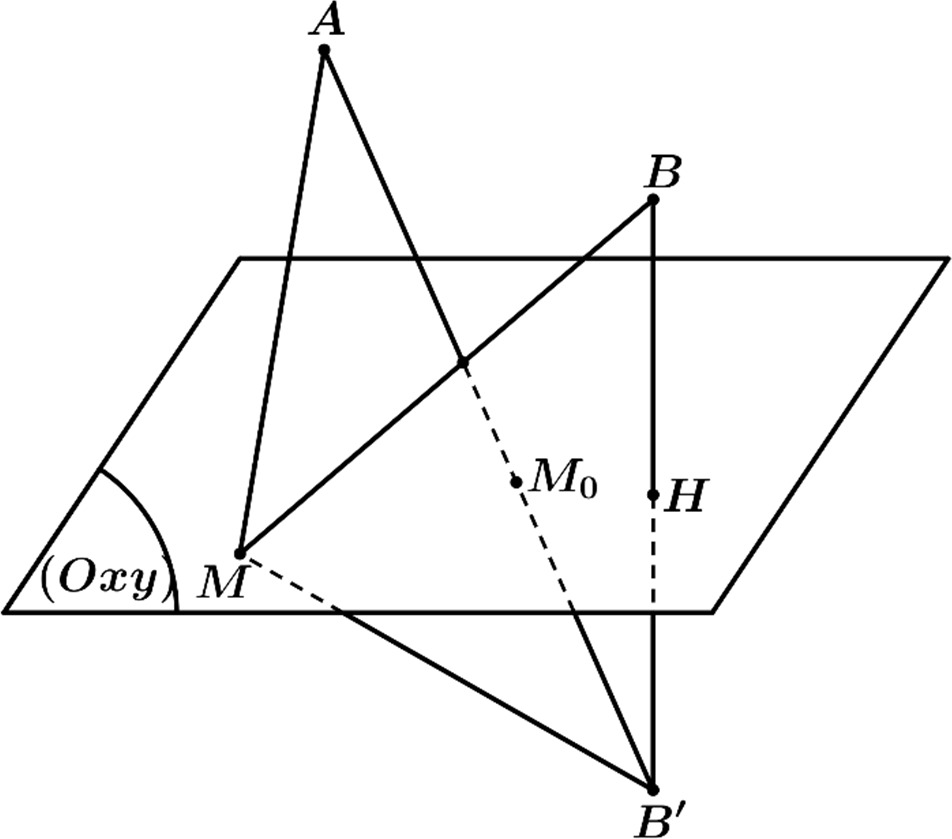
Bài toán trở về khi $MA+MB$ là nhỏ nhất thì ta cần tính $OM$.
Gọi $H$ là hình chiếu của điểm $B$ xuống mặt phẳng $\left(Oxy\right)$ và $B’$ là điểm đối xứng của $B$ qua mặt phẳng $\left(Oxy\right)$.
Khi đó $H\left(-100;100;0\right)$ suy ra $B’\left(-100;100;-40\right)$
Ta có: $MA+MB=MA+M{B}’\ge A{B}’$. Dấu bằng xảy ra khi $M\equiv{M_0}\left(a;b;0\right)$
Khi đó: $\overrightarrow{A{M_0}}=\left(a-200;b+200;-50\right)$ ; $\overrightarrow{A{B}’}=\left(-300;300;-90\right)$
Do $\overrightarrow{A{M_0}}\parallel\overrightarrow{A{B}’}$ nên $\dfrac{a-200}{-300}=\dfrac{b+200}{300}=\dfrac{5}{9}\Rightarrow\left[\begin{array}{l} a=\dfrac{100}{3}\\ b=-\dfrac{100}{3}\end{array}\right.\Rightarrow{M_0}\left(\dfrac{100}{3};-\dfrac{100}{3};0\right)$
Vậy $O{M_0}=\sqrt{\left(\dfrac{100}{3}\right)^2+\left(-\dfrac{100}{3}\right)^2+0^2}\approx 47$ nên khoảng cách từ vị trí người quan sát đến địa điểm thả hai quả bóng bay này khoảng $47$ mét.
