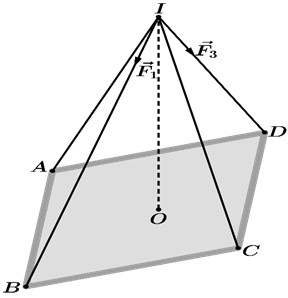
Trong không gian với hệ trục tọa độ $Oxyz$, một tấm bảng đồng chất có dạng hình vuông $ABCD$ tâm $O$ được treo nghiêng bởi 4 sợi dây $IA,IB,IC,ID$ gắn cố định tại điểm $I\left(0;0;9\right)$ như hình vẽ. Điểm $O\left(0;0;5\right)$ ; $A\left(-\sqrt{2};\sqrt{2};5\right)$ và góc $\widehat{OID}$ đạt giá trị lớn nhất. Gọi $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3},\overrightarrow{F_4}$ lần lượt là lực căng của các sợi dây $IB,IC,ID,IA$. Biết rằng $\left|\overrightarrow{F_1}\right|=50$ N và $\left|\overrightarrow{F_2}\right|=40$ N
Tính khối lượng $m$ (kg) của tấm bảng (Kết quả làm tròn đến hàng đơn vị) (Cho gia tốc trọng trường $g=9,8$ (m/s2) và trọng lượng của tấm bẳng được tính bằng công thức $P=m.g$)
Đáp án: 15
Lời giải: Do $O$ là trung điểm của $AC$ nên $C\left(\sqrt{2};-\sqrt{2};5\right)$ và gọi $D\left(a;b;c\right)$
Khi đó $\overrightarrow{OD}=\left(a;b;c-5\right)$ ; $\overrightarrow{AC}=\left(2\sqrt{2};-2\sqrt{2};0\right)$ mà hai vectơ này vuông góc với nhau
Từ đó $2\sqrt{2}a=2\sqrt{2}b\Leftrightarrow a=b\Rightarrow\overrightarrow{DC}=\left(a-\sqrt{2};a+\sqrt{2};c-5\right);\overrightarrow{DA}=\left(a+\sqrt{2};a-\sqrt{2};c-5\right)$
Ta có: $\overrightarrow{ID}=\left(a;a;\sqrt{4-2a^2}-4\right);\overrightarrow{IO}=\left(0;0;-4\right)\Rightarrow\cos\widehat{OID}=\dfrac{16-4\sqrt{4-2a^2}}{16\sqrt{a^2+a^2+\left(4-4\sqrt{4-2a^2}\right)^2}}$
Khảo sát hàm số $f(a)=\dfrac{16-4\sqrt{4-2a^2}}{16\sqrt{a^2+a^2+\left(4-4\sqrt{4-2a^2}\right)^2}}$ tìm được $a=\dfrac{\sqrt{6}}{2}$
Vậy tọa độ các điểm: $A\left(-\sqrt{2};\sqrt{2};5\right)$ ; $B\left(-\dfrac{\sqrt{6}}{2};-\dfrac{\sqrt{6}}{2};1\right)$ ; $C\left(\sqrt{2};-\sqrt{2};5\right)$ ; $D\left(\dfrac{\sqrt{6}}{2};\dfrac{\sqrt{6}}{2};6\right)$
Ta có: $\overrightarrow{IA}=\left(-\sqrt{2};\sqrt{2};-4\right)\Rightarrow\left|\overrightarrow{IA}\right|=2\sqrt{5}$ ; $\overrightarrow{IC}=\left(\sqrt{2};-\sqrt{2};-4\right)\Rightarrow\left|\overrightarrow{IC}\right|=2\sqrt{5}$
Vậy $\left|\overrightarrow{F_4}\right|=\left|\overrightarrow{F_2}\right|=k.2\sqrt{5}=40\Rightarrow k=4\sqrt{5}$
Suy ra $\overrightarrow{F_2}=\left(-4\sqrt{10};4\sqrt{10};-16\sqrt{5}\right)$ ; $\overrightarrow{F_4}=\left(4\sqrt{10};-4\sqrt{10};-16\sqrt{5}\right)$
Tương tự $\overrightarrow{IB}=\left(-\dfrac{\sqrt{6}}{2};-\dfrac{\sqrt{6}}{2};-5\right)\Rightarrow\left|\overrightarrow{IB}\right|=2\sqrt{7}$ ; $\overrightarrow{ID}=\left(\dfrac{\sqrt{6}}{2};\dfrac{\sqrt{6}}{2};-3\right)\Rightarrow\left|\overrightarrow{ID}\right|=2\sqrt{3}$
Sử dụng tỉ lệ giữa độ dài dây và độ lớn lực: $\dfrac{\left|\overrightarrow{F_1}\right|}{\left|\overrightarrow{F_3}\right|}=\dfrac{2\sqrt{7}}{2\sqrt{3}}\Rightarrow\left|\overrightarrow{F_3}\right|=\dfrac{50\sqrt{21}}{7}$
Suy ra $\overrightarrow{F_3}=\left(\dfrac{25\sqrt{42}}{14};-\dfrac{25\sqrt{42}}{14};-\dfrac{75\sqrt{7}}{7}\right)$ ; $\overrightarrow{F_1}=\left(-\dfrac{25\sqrt{42}}{14};-\dfrac{25\sqrt{42}}{14};-\dfrac{125\sqrt{7}}{7}\right)$
Để hệ cân bằng thì $\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\overrightarrow{F_4}=\overrightarrow{P}=\left(0;0;-32\sqrt{5}-\dfrac{200\sqrt{7}}{7}\right)\Rightarrow\left| P\right|=\dfrac{200\sqrt{7}}{7}+32\sqrt{5}$
Vậy khối lượng của thanh kim loại là: $m=\dfrac{P}{g}=\dfrac{\dfrac{200\sqrt{7}}{7}+32\sqrt{5}}{9,8}=15,015\approx 15$ (kg)
