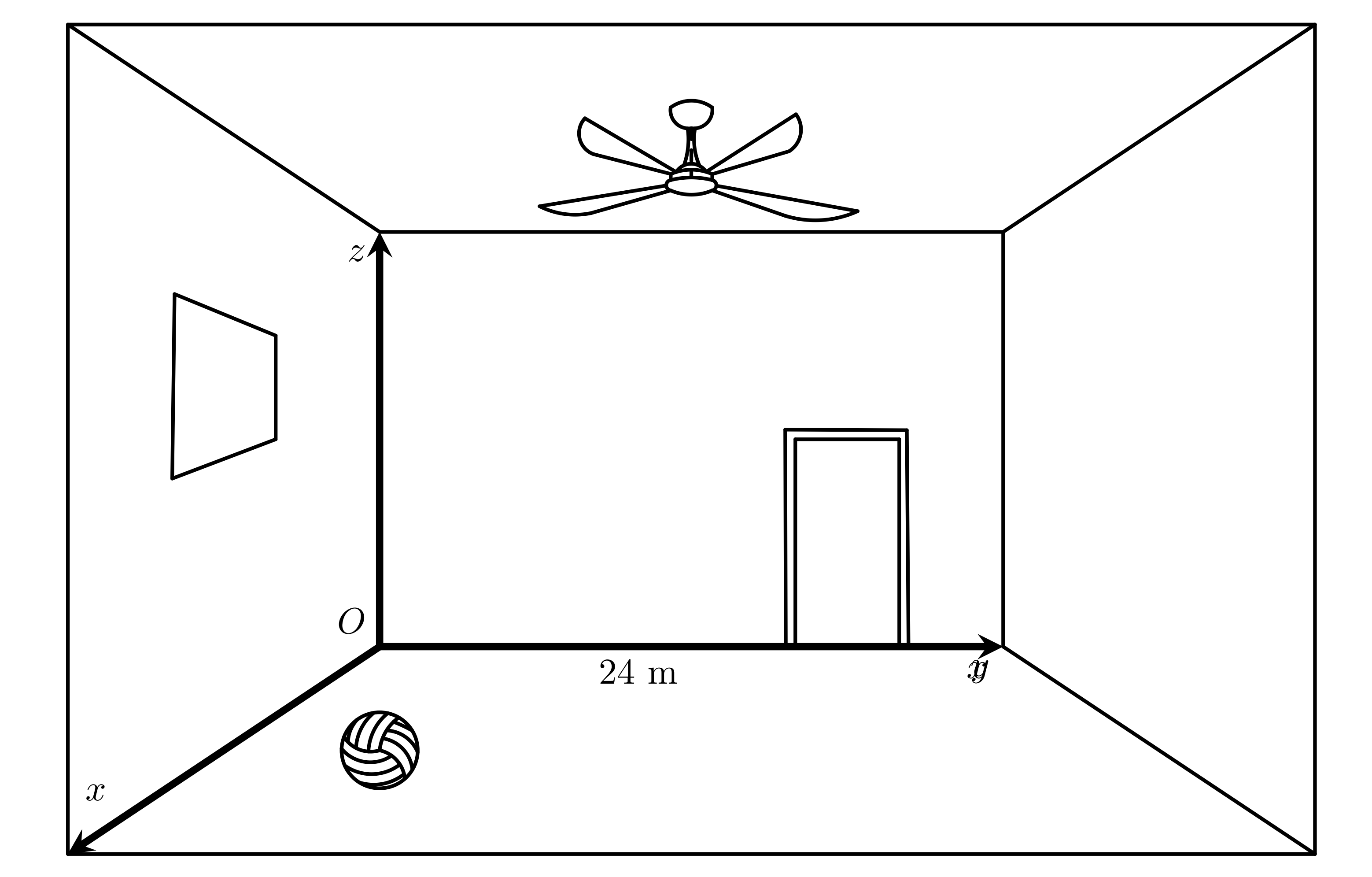
Trong một căn phòng dạng hình hộp chữ nhật với chiều dài $24$ m, rộng $18$ m và cao $12$ m có một cây quạt trần $A$ ở vị trí tâm trần nhà và một quả bóng $B$ nằm trên sàn. Chọn hệ trục tọa độ như hình vẽ (đơn vị: m). Biết quả bóng cách tường $Oxz$ một khoảng bằng $9$ m và cách tường $(Oyz)$ một khoảng bằng $6$ m. Nếu cây quạt trần đột nhiên rơi xuống sàn thì vị trí chạm sàn của cây quạt cách quả bóng bao nhiêu?
Đáp án: 6
Lời giải: Căn phòng có chiều dài $24$ m, chiều rộng $18$ m và cao $12$ m.
Cây quạt trần $A$ nằm ở vị trí tâm trần nhà. Do đó, tọa độ của cây quạt trần $A$ là $A \left( \dfrac{24}{2}; \dfrac{18}{2}; 12 \right)$ hay $A(12;9;12)$.
Quả bóng nằm trên sàn, cách tường $(Oxz)$ $9$ m, tức là tung độ $y=9$.
Quả bóng cũng cách tường $(Oyz)$ $6$ m, tức là hoành độ $x=6$.
Quả bóng nằm trên sàn nhà nên cao độ bằng $z=0$
Suy ra tọa độ của bóng là $B(6;9;0)$
Khi cây quạt rơi xuống sàn, vị trí chạm sàn của cây quạt sẽ có cùng hoành độ $x$ và tung độ $y$ như tọa độ của cây quạt khi ở trên trần, chỉ có cao độ $z$ thay đổi thành $0$ (vì nằm trên sàn) (tức là hình chiếu vuông góc của điểm $A$ lên mặt phẳng $(Oxy)$).
Vị trí chạm sàn của cây quạt có tọa độ là $A'(12;9;0)$.
Ta có $\overrightarrow{A’B}=(-6; 0; 0)$.
Vậy khoảng cách từ vị trí chạm sàn của cây quạt đến quả bóng là $6$ m.
