Trong Hóa học, cấu tạo của phân tử ammoniac ($\mathrm{NH}_3$) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen ($\mathrm{N}$) và đáy là tam giác $H_1H_2H_3$ với $H_1$, $H_2$, $H_3$ là vị trí của ba nguyên tử hydrogen ($\mathrm{H}$)

Trong Hóa học, cấu tạo của phân tử ammoniac ($\mathrm{NH}_3$) có dạng hình chóp tam giác đều mà đỉnh là nguyên tử nitrogen ($\mathrm{N}$) và đáy là tam giác $H_1H_2H_3$ với $H_1$, $H_2$, $H_3$ là vị trí của ba nguyên tử hydrogen ($\mathrm{H}$). Góc tạo bởi liên kết $\mathrm{H}-\mathrm{N}-\mathrm{H}$, có hai cạnh là hai đoạn thẳng nối $N$ với hai trong ba điểm $H_1$, $H_2$, $H_3$ (chẳng hạn $\widehat{H_1NH_2}$), gọi là góc liên kết của phân tử $\mathrm{NH}_3$. Góc này xấp xỉ $107^{\circ}$.

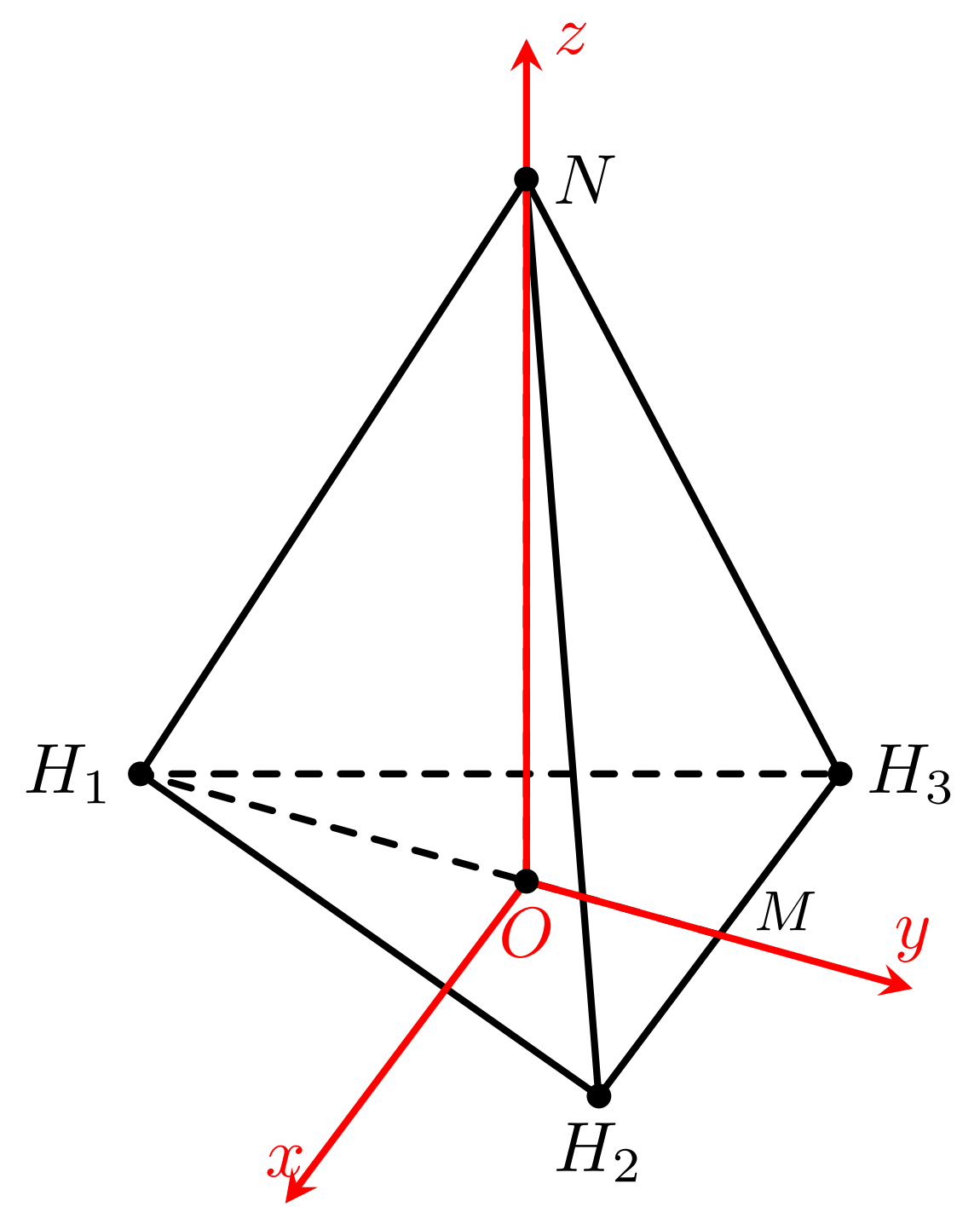
Trong không gian $Oxyz$, cho một phân tử $\mathrm{NH}_3$ được biểu diễn bởi hình chóp tam giác đều $N.H_1H_2H_3$ với $O$ là tâm của đáy. Nguyên tử nitrogen được biểu diễn bởi điểm $N$ thuộc trục $Oz$, ba nguyên tử hydrogen ở các vị trí $H_1$, $H_2$, $H_3$ trong đó $H_1(0;-2;0)$ và $H_2H_3$ song song với trục $Ox$. Tính khoảng cách giữa hai nguyên tử nitrogen với mỗi nguyên tử hydrogen (làm tròn các kết quả tính toán đến hàng phần trăm).
Đáp án: 2,15
Lời giải: Gọi $y$ là khoảng cách giữa hai nguyên tử nitrogen với mỗi nguyên tử hydrogen; khi đó $NH_2=y$.
Vì $H_1(0;-2;0)$ nên
$O H_1=2 \Rightarrow M H_1=\frac{3}{2} O H_1=3 \Rightarrow H_1 H_2=H_2 H_3=H_3 H_1=\dfrac{M H_1}{\frac{\sqrt{3}}{2}}=2 \sqrt{3}.$
Áp dụng định lí cosin ta có $H_1H_2^2=NH_1^2+NH_2^2-2\cdot NH_1\cdot NH_2\cos \widehat{H_1NH_2}\Leftrightarrow 2y^2-2y^2\cos 107^\circ=12$ $\Leftrightarrow y^2=\dfrac{12}{2-2\cos 107^\circ}\Leftrightarrow y\approx2{,}15.$