Biết góc quan sát ngang của một camera là $116^\circ$. Trong không gian $Oxyz$, camera được đặt tại điểm $A(2;1;5)$ và chiếu thẳng về phía mặt phẳng $(P)\colon 2x-y-2z+13=0$. Hỏi vùng quan sát được trên mặt phẳng $(P)$ của camera là hình tròn có đường kính bằng bao nhiêu (\textit {làm tròn kết quả đến hàng phần mười})?
\par

Đáp án: 6,4
Lời giải: Hình vẽ minh hoạ
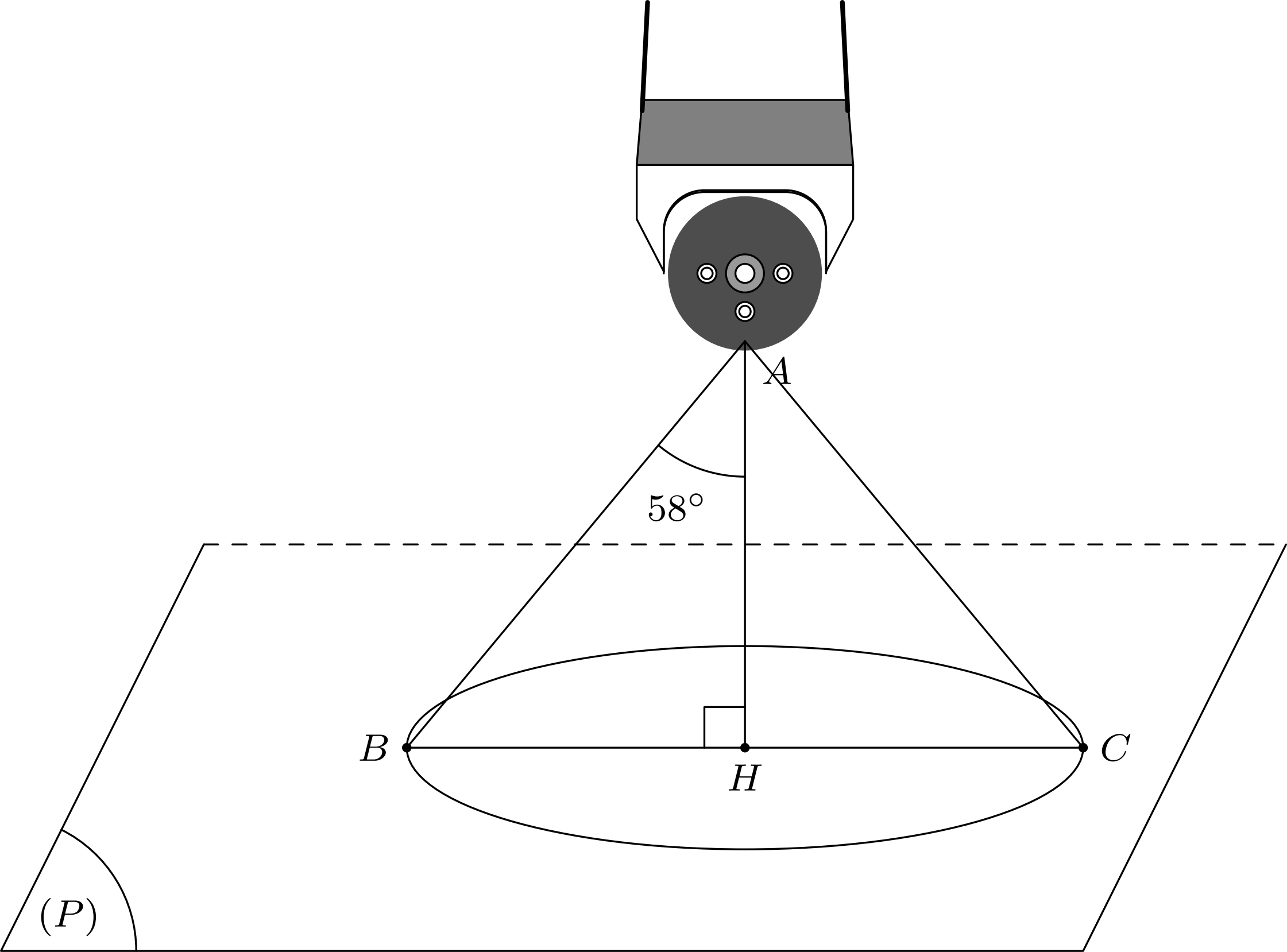
Gọi $A$, $B$, $C$ là các điểm như hình vẽ bên dưới và $H$ là hình chiếu vuông góc của $A$ lên mặt phẳng $(P)$.
Theo đề
$\widehat{BAC}=116^\circ \Rightarrow \widehat{BAH}=58^\circ$.
Khi đó
$AH=\mathrm{d}\big(A,(P)\big) =\dfrac{\left|2\cdot 2-1-2\cdot 5+13\right|}{\sqrt{4+1+4}} =2$ (đvđd).
Xét tam giác $ABH$ vuông tại $H$, ta có
$\tan \widehat{BAH}=\dfrac{BH}{AH} \Rightarrow BH=\tan 58^\circ \cdot 2=2\tan 58^\circ \text{(đvđd)}. $
Suy ra $BC=2BH=2\cdot 2\tan 58^\circ \approx 6{,}4$ (đvđd).
Vậy vùng quan sát của camera trên mặt phẳng $(P)$ là hình tròn có đường kính khoảng $6{,}4$ (đvđd).
