[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} - 2x - 8\,,\,\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { - {x^3} + 12x + m} \right)\) có đúng hai điểm cực trị thuộc khoảng \(\left( {0\,;\,5} \right)\)? A. \(5\) . B. \(6\) . C. \(7\) … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 2x – 8\,,\,\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( { – {x^3} + 12x + m} \right)\) có đúng hai điểm cực trị thuộc khoảng \(\left( {0\,;\,5} \right)\)?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 2x\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( { – 2;4} \right)\)?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} - 2x\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2} + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( { - 2;4} \right)\)? A. \(3\). B. \(4\). C. \(5\). D. … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 2x\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( { – 2;4} \right)\)?
[Mức độ 4] Xét các số thực dương \(x,\,\,y\) thỏa mãn \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} – {x^2}{y^2} – 2{y^2}x\). Khi biểu thức \(4y – {x^2}\) đạt giá trị lớn nhất thì giá trị của biểu thức \(3x + 2y\) bằng
[Mức độ 4] Xét các số thực dương \(x,\,\,y\) thỏa mãn \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} - {x^2}{y^2} - 2{y^2}x\). Khi biểu thức \(4y - {x^2}\) đạt giá trị lớn nhất thì giá trị của biểu thức \(3x + 2y\) bằng A. \(\frac{{11}}{2}\). B. \(\frac{7}{2}\). C.\(3\). D. \(4\). Lời giải: *) Ta có: \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} - … [Đọc thêm...] về[Mức độ 4] Xét các số thực dương \(x,\,\,y\) thỏa mãn \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} – {x^2}{y^2} – 2{y^2}x\). Khi biểu thức \(4y – {x^2}\) đạt giá trị lớn nhất thì giá trị của biểu thức \(3x + 2y\) bằng
[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = x{\left( {x – 1} \right)^2}\left( {x – 4} \right).\) Có bao nhiêu giá trị nguyên của tham số m để hàm số \(g\left( x \right) = f\left( {{x^2} + m} \right)\) có 3 điểm cực trị.
[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x - 1} \right)^2}\left( {x - 4} \right).\) Có bao nhiêu giá trị nguyên của tham số m để hàm số \(g\left( x \right) = f\left( {{x^2} + m} \right)\) có 3 điểm cực trị. A. \(0\). B. \(4\). C. \(3\). D. \(2\). Lời giải Ta có \(f'\left( x \right) = x{\left( {x - 1} … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = x{\left( {x – 1} \right)^2}\left( {x – 4} \right).\) Có bao nhiêu giá trị nguyên của tham số m để hàm số \(g\left( x \right) = f\left( {{x^2} + m} \right)\) có 3 điểm cực trị.
Cho hàm số \(y = f(x)\) có đạo hàm \({f^\prime }(x) = {(x – 1)^2}\left( {{x^2} – 3x} \right)\), với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g(x) = f\left( {{x^2} – 4x + m} \right)\) có 5 điểm cực trị thuộc khoảng \(\left( {1;4} \right)\)?
Cho hàm số \(y = f(x)\) có đạo hàm \({f^\prime }(x) = {(x - 1)^2}\left( {{x^2} - 3x} \right)\), với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g(x) = f\left( {{x^2} - 4x + m} \right)\) có 5 điểm cực trị thuộc khoảng \(\left( {1;4} \right)\)? A.\(2\). B. \(0\). C. vô số. D. \(5\). Lời giải: Ta có \(f'(x) = {(x - … [Đọc thêm...] vềCho hàm số \(y = f(x)\) có đạo hàm \({f^\prime }(x) = {(x – 1)^2}\left( {{x^2} – 3x} \right)\), với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g(x) = f\left( {{x^2} – 4x + m} \right)\) có 5 điểm cực trị thuộc khoảng \(\left( {1;4} \right)\)?
[Mức độ 4] Cho hai hàm số \(y = {x^6} + 6{x^4} + 6{x^2} + 1\) và \(y = {x^3}\sqrt {m – 15x} \left( {m + 3 – 15x} \right)\) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\). Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 2024;2024} \right]\) để \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp \(S\) bằng
[Mức độ 4] Cho hai hàm số \(y = {x^6} + 6{x^4} + 6{x^2} + 1\) và \(y = {x^3}\sqrt {m - 15x} \left( {m + 3 - 15x} \right)\) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\). Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2024;2024} \right]\) để \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) cắt … [Đọc thêm...] về[Mức độ 4] Cho hai hàm số \(y = {x^6} + 6{x^4} + 6{x^2} + 1\) và \(y = {x^3}\sqrt {m – 15x} \left( {m + 3 – 15x} \right)\) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\). Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 2024;2024} \right]\) để \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp \(S\) bằng
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {\left( {x – 1} \right)^2}\left( {{x^2} – 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} – 8x + m} \right)\) có \(5\) điểm cực trị?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^2}\left( {{x^2} - 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} - 8x + m} \right)\) có \(5\) điểm cực trị? A. \(15\). B. \(17\). C. \(16\) D. \(18\) Lời giải: Đặt \(g\left( x … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {\left( {x – 1} \right)^2}\left( {{x^2} – 2x} \right)\) với \(\forall x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(f\left( {{x^2} – 8x + m} \right)\) có \(5\) điểm cực trị?
[ Mức độ 3] Cho Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( {2{x^3} – 6x + 1} \right) + 3 = m\) có \(7\)nghiệm phân biệt.

[ Mức độ 3] Cho Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( {2{x^3} - 6x + 1} \right) + 3 = m\) có \(7\)nghiệm phân biệt. A. \(6\). B. \(7\). C. \(8\). D. \(9\) Lời giải: Đặt \(t = 2{x^3} - 6x + 1\) . \( \Rightarrow t' = 6{x^2} - 6 = 0 \Leftrightarrow x = \pm … [Đọc thêm...] về[ Mức độ 3] Cho Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( {2{x^3} – 6x + 1} \right) + 3 = m\) có \(7\)nghiệm phân biệt.
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \(OO’ = 5\)\({\rm{cm}}\), \(OA = 10\)\({\rm{cm}}\), \(OB = 20\) \({\rm{cm}}\), đường cong \(AB\) là một phần của parabol có đỉnh là điểm\(A\). Thể tích của chiếc mũ bằng
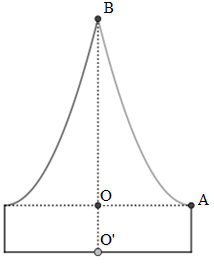
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \(OO' = 5\)\({\rm{cm}}\), \(OA = 10\)\({\rm{cm}}\), \(OB = 20\) \({\rm{cm}}\), đường cong \(AB\) là một phần của parabol có đỉnh là điểm\(A\). Thể tích của chiếc mũ bằng A. … [Đọc thêm...] vềChuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \(OO’ = 5\)\({\rm{cm}}\), \(OA = 10\)\({\rm{cm}}\), \(OB = 20\) \({\rm{cm}}\), đường cong \(AB\) là một phần của parabol có đỉnh là điểm\(A\). Thể tích của chiếc mũ bằng
Cho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\)
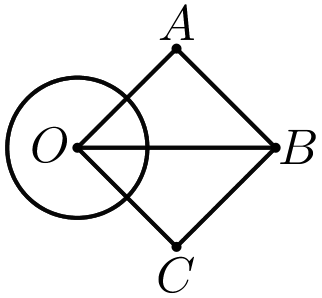
Cho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\) A. \(V = \frac{{8\left( {3 + 4\sqrt 2 } \right)\pi }}{3}.\) B. \(V = \frac{{8\left( {2 + 5\sqrt 2 } \right)\pi }}{3}.\) C. \(V = \frac{{8\left( {3 + … [Đọc thêm...] vềCho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\)
