Xét phần đựng nước bên trong một lục bình có dạng mặt tròn xoay trong đó đường sinh là đường cong $\left(C\right)$ quay quanh trục $\left(d\right)$ như hình bên. Biết rằng $\left(C\right)$ là đường cong bậc ba; chiều cao phần đựng nước là 35 cm

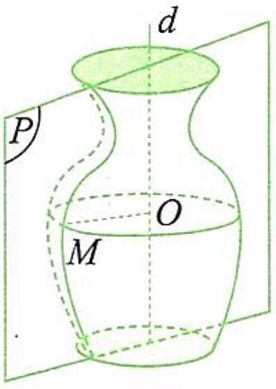
Bài toán: Xét phần đựng nước bên trong một lục bình có dạng mặt tròn xoay trong đó đường sinh là đường cong $\left(C\right)$ quay quanh trục $\left(d\right)$ như hình bên. Biết rằng $\left(C\right)$ là đường cong bậc ba; chiều cao phần đựng nước là 35 cm ; bán kính đáy phần đựng nước là 10 cm ; bán kính miệng phần đựng nước là $14,375\mathrm{\,\;cm}$; chỗ rộng nhất của phần đựng nước có bán kính 30 cm ; độ cao của phần đựng nước tính từ đáy đến chỗ rộng nhất là 10 cm . Thể tích tối đa mà chiếc bình này đựng được là bao nhiêu lít? (kết quả

 làm tròn đến hàng phần chục)

Lòi giải

Trả lòi: 49,1.
Đổi đơn vị về đềximét. Ta có thể minh hoạ đường $\mathrm{\,sinh}\left(C\right)$ và trục quay $d$ như hình bên.

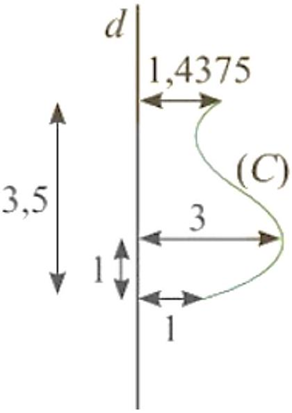
Gắn hệ trục như hình vẽ (trục quay $d$ là trục hoành, trục tung cắt đường sinh tại điểm thuộc phần rộng nhất).

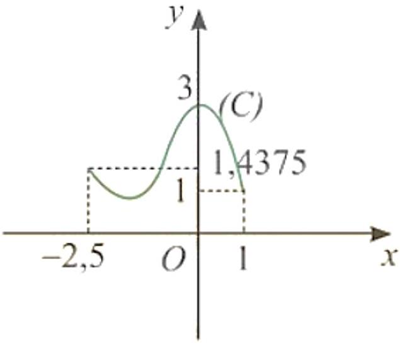
Đặt $\left(C\right):y=f\left(x\right)=ax^{3}+bx^{2}+cx+d$. Dựa vào đồ thị ta thấy

$\begin{array}{*{20}{r}}{}&\left\{\begin{array}{*{20}{c}}f’\left(0\right)=0\\f\left(0\right)=3\\f\left(1\right)=1\\f\left(-2,5\right)=1,4375\end{array}\Leftrightarrow \left\{\begin{array}{*{20}{c}}c=0\\d=3\\a+b+c+d=1\\-15,625a+6,25b-2,5c+d=1,4375\end{array}\right. \right. \\{}&y=f\left(x\right)=-0,5x^{3}-1,5x^{2}+3.\end{array}\Leftrightarrow \left\{\begin{array}{*{20}{l}}a=-0,5\\b=-1,5\\c=0\\d=3.\end{array}\right. $

Khi đó thể tích phần chứa nước chính là thể tích khối tròn xoay tạo thành khi quay phần hình phẳng bị giới hạn bởi $\left(C\right):y=f\left(x\right)$, trục hoành, các đường thẳng $x=-2,5;x=1$ quanh trục hoành. Do đó thể tích này bằng