Một vật chuyển động thẳng. Khi vật bắt đầu qua điểm $O$, người ta bắt đầu quan sát, đo đạc chuyển động của vật thì thấy vận tốc tức thời của vật tại thời điểm $t\left(s\right)$ là $v\left(t\right)\left(\mathrm{\,m}/\mathrm{\,s}\right)$, hàm vận tốc $v\left(t\right)$ có đồ thị phụ thuộc thời gian là một phần của đường parabol đỉnh $I\left(\dfrac{4}{3};-\dfrac{7}{3}\right)$ như hình bên (với $t\geq 0$ và mốc tính thời gian là lúc bắt đầu quan sát chuyển động)

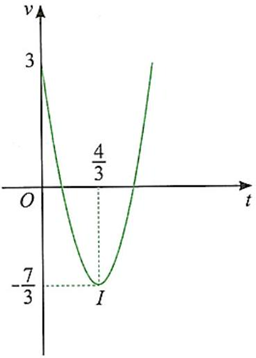
Bài toán: Một vật chuyển động thẳng. Khi vật bắt đầu qua điểm $O$, người ta bắt đầu quan sát, đo đạc chuyển động của vật thì thấy vận tốc tức thời của vật tại thời điểm $t\left(s\right)$ là $v\left(t\right)\left(\mathrm{\,m}/\mathrm{\,s}\right)$, hàm vận tốc $v\left(t\right)$ có đồ thị phụ thuộc thời gian là một phần của đường parabol đỉnh $I\left(\dfrac{4}{3};-\dfrac{7}{3}\right)$ như hình bên (với $t\geq 0$ và mốc tính thời gian là lúc bắt đầu quan sát chuyển động). Tính tổng quãng đường vật đi được từ lúc đầu đến lúc vật trở lại điểm $O$ lần cuối cùng (kết quả tính bằng mét và làm tròn đến hàng phần trăm).

Lòi giải

Trả lòi: 5,49.

Dựa vào đồ thị ta thấy

$\begin{array}{*{20}{r}}{}&v\left(t\right)=at^{2}+bt+c;\left\{\begin{array}{*{20}{c}}c=3\\\dfrac{-b}{2a}=\left(\dfrac{4}{3}\right)\\a\cdot (\dfrac{4}{3})^{2}+b\cdot \left(\dfrac{4}{3}\right)+c=-\dfrac{7}{3}\end{array}\Rightarrow \left\{\begin{array}{*{20}{c}}a=3\\b=-8\\c=3\end{array}\Rightarrow v\left(t\right)=3t^{2}-8t+3\right. \right. \\{}&{}\end{array}$

Tại các thời điểm vật qua $O$ ứng với $t$ thoả mãn $s\left(t\right)=0\Leftrightarrow \left[\begin{array}{*{20}{l}}t=0\\t=3\end{array}\right. $

Do đó thời điểm cuối vật qua $O$ là $t=3\left(s\right)$. Nên tổng quảng đường vật đi được từ lúc đầu đến lúc vật trở lại điểm $O$ lần cuối cùng .