Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình. Khí bên trong ống được duy trì ở ${150^{\circ} {C}}$. Biết rằng nhiệt độ ${T\left({ }^{\circ} {C}\right)}$ tại điểm ${{A}}$ trên thành ống là hàm số của khoảng cách ${x({~cm})}$ từ ${{A}}$ đến tâm của mặt cắt và ${T^{\prime}(x)=-\frac{30}{x} (6 \leq x \leq 8) . }$ 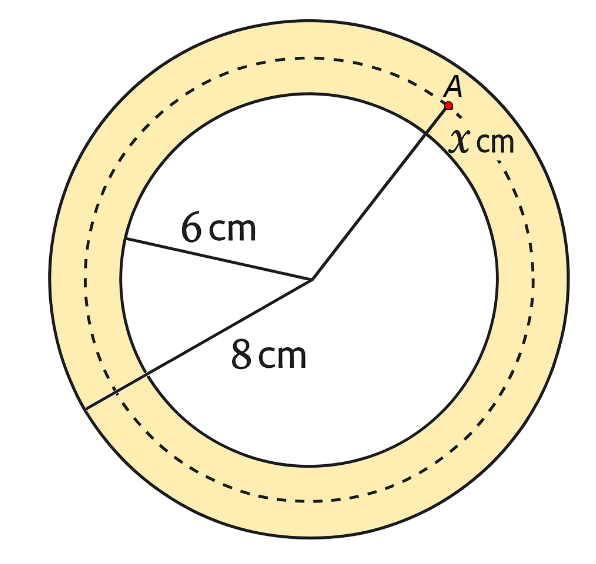 Tìm nhiệt độ mặt ngoài của ống. (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm). Lời
Tìm nhiệt độ mặt ngoài của ống. (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần trăm). Lời
Lời giải Do nhiệt độ của khí bên trong ống luôn được duy trì ở ${150^{\circ} {C}}$, nên ${T(6)=150}$. Nhiệt độ mặt ngoài của ống là ${T(8)=[T(8)-T(6)]+T(6)=\int\limits_6^8 T^{\prime}(x) d x+T(6)}$. Ta có ${\int\limits_6^8 T^{\prime}(x) d x=\int\limits_6^8-\frac{30}{x} d x=-30 \int\limits_6^8 \frac{1}{x} d x=-\left.30 \cdot(\ln |x|)\right|_6 ^8=-30 \ln 8+30 \ln 6}$.
Vậy nhiệt độ bên ngoài mặt ống là ${T(8)=-30 \ln 8+30 \ln 6+150 \approx 141,37^{\circ} C}$
Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình
Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân
