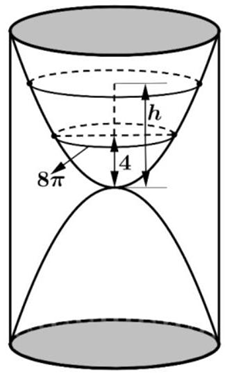
Một chiếc đồng hồ cát như hình vẽ gồm hai phần đối xứng nhau qua mặt phẳng nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai parabol chung đỉnh và đối xứng nhau qua mặt phằng nằm ngang.
Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân

