Một biển quảng cáo có dạng hình vuông $ABCD$ cạnh $AB=4\mathrm{\,\;m}$. Trên tấm biển đó có các đường tròn tâm $A$ và đường tròn tâm $B$ cùng bán kính $R=4\mathrm{\,\;m}$, hai đường tròn cắt nhau như hình vẽ

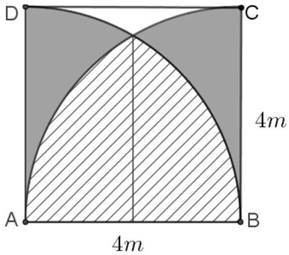
Bài toán: Một biển quảng cáo có dạng hình vuông $ABCD$ cạnh $AB=4\mathrm{\,\;m}$. Trên tấm biển đó có các đường tròn tâm $A$ và đường tròn tâm $B$ cùng bán kính $R=4\mathrm{\,\;m}$, hai đường tròn cắt nhau như hình vẽ. Chi phí để sơn phần gạch chéo là 150000 đồng $/\mathrm{\,m}^{2}$, chi phí sơn phần màu đen là 100000 đồng/ $\mathrm{\,m}^{2}$ và chi phí để sơn phần còn lại là 250000 đồng $/\mathrm{\,m}^{2}$

Hỏi số tiền để sơn biển quảng cáo theo cách trên (Đơn vị: triệu đồng và kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy)?

Lòi giải

Gọi $I$ là giao điểm của 2 cung tròn $AC;BD$. Chọn gốc toạ độ $A\left(0;0\right)\Rightarrow B\left(4,0\right)$
Xét cung tròn có phương trình $y=\sqrt {16-x^{2}} $
Phần diện tích gạch chéo
Phần diện tích màu đen: $2.\left(\dfrac{1}{4}\pi \cdot 4^{2}-\dfrac{16\pi }{3}+4\sqrt {3} \right)=\dfrac{-8\pi }{3}+8\sqrt {3} $
Phần diện tích còn lại: $16-\left(\dfrac{16\pi }{3}-4\sqrt {3} +\dfrac{-8\pi }{3}+8\sqrt {3} \right)=16-\dfrac{8\pi }{3}-4\sqrt {3} $
Số tiền để sơn biển quảng cáo:

$\left( \frac{16\pi }{3}-4\sqrt{3} \right)\cdot 150000+\left( \frac{-8\pi }{3}+8\sqrt{3} \right)\cdot 100000+$            $\left( 16-\frac{8\pi }{3}-4\sqrt{3} \right)\cdot 250000\approx 2,2\text{ }\!\!~\!\!\text{ tri}\text{u }\!\!~\!\!\text{ }\text{ng}\text{. }\!\!~\!\!\text{ }$