Cho hình lăng trụ \(ABC.A’B’C’\) có tam giác \(ABC\) vuông tại \(A\). \(AB = a\), \(AC = a\sqrt 3 \), \(AA’ = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A’B’C’} \right)\) trung với trung điểm \(H\) của đoạn \(B’C’\). Khoảng cách giữa hai đường thẳng \(AA’\) và \(BC’\) bằng

Cho hình lăng trụ \(ABC.A’B’C’\) có tam giác \(ABC\) vuông tại \(A\). \(AB = a\), \(AC = a\sqrt 3 \), \(AA’ = 2a\). Hình chiếu vuông góc của điểm \(A\) trên mặt phẳng \(\left( {A’B’C’} \right)\) trung với trung điểm \(H\) của đoạn \(B’C’\) (tham khảo hình vẽ dưới đây). Khoảng cách giữa hai đường thẳng \(AA’\) và \(BC’\) bằng

A. \(\frac{{a\sqrt 5 }}{3}\).
B. \(\frac{{a\sqrt {15} }}{5}\).
C. \(\frac{{a\sqrt 5 }}{5}\).
D. \(\frac{{a\sqrt {15} }}{3}\).
Lời giải

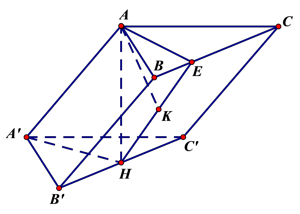
\(AA’//\left( {BCC’A’} \right)\)\( \Rightarrow \)\(d\left( {AA’,\,BC’} \right) = d\left( {AA’,\,\left( {BCC’B’} \right)} \right) = d\left( {A,\,\left( {BCC’B’} \right)} \right)\).
Dựng \(AE\) vuông góc với \(BC\) tại \(E\). Lúc đó \(\left( {AHE} \right) \bot \left( {BCC’B’} \right)\).
Dựng \(AK\) vuông góc với \(EH\) tại \(K\). Lúc đó \(AK \bot \left( {BCC’B’} \right)\).
Do đó \(d\left( {AA’,\,BC’} \right) = AK\).
Tính \(AK\):
Vì ba cạnh \(AB,\,AC,\,AH\) đôi một vuông góc và \(AK \bot \left( {BCH} \right)\) nên ta có
\(\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} + \frac{1}{{A{H^2}}}\)\( = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \frac{1}{{A{H^2}}} = \frac{4}{{3{a^2}}} + \frac{1}{{A{H^2}}}\).
Ta lại có \(A{H^2} = A'{A^2} – A'{H^2}\).
Vì tam giác \(A’B’C’\) vuông tại \(A’\) và có \(H\) là trung điểm của \(B’C’\) nên \(A’H = \frac{{B’C’}}{2}\).
Ta có \(B’C’ = BC = \sqrt {A{B^2} + B{C^2}} = 2a\) do đó \(A’H = a\) suy ra \(A{H^2} = A'{A^2} – A'{H^2} = 3{a^2}\).
\(\frac{1}{{A{K^2}}} = \frac{4}{{3{a^2}}} + \frac{1}{{A{H^2}}} = \frac{4}{{3{a^2}}} + \frac{1}{{3{a^2}}} = \frac{5}{{3{a^2}}}\)\( \Rightarrow AK = \frac{{a\sqrt {15} }}{5}\).
Vậy \(d\left( {AA’,\,BC’} \right) = \frac{{a\sqrt {15} }}{5}\).