Lý thuyết Ôn tập Nguyên Hàm – Tích Phân Và Ứng Dụng

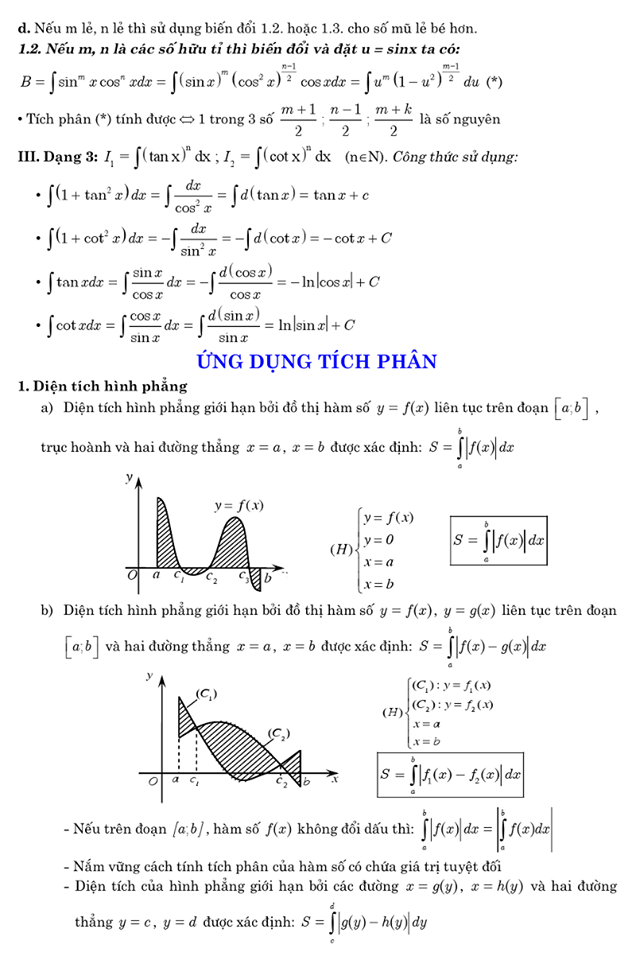
Lý thuyết Ôn tập Nguyên Hàm – Tích Phân Và Ứng Dụng

Đây là các công thức cần nhớ.

===== 














==============