Xét các số thực dương \(x,{\rm{ }}y\) thỏa mãn \({\log _{\sqrt 3 }}\frac{{2x + y}}{{4{x^2} + {y^2} + 2xy + 2}} = 2x\left( {2x – 3} \right) + y\left( {y – 3} \right) + 2xy\). Tìm giá trị lớn nhất của \(P = \frac{{6x + 2y + 1}}{{2x + y + 6}}\). A. \(2\). B. \(1\). C. \(3\). D. \(4\).

Xét các số thực dương \(x,{\rm{ }}y\) thỏa mãn
\({\log _{\sqrt 3 }}\frac{{2x + y}}{{4{x^2} + {y^2} + 2xy + 2}} = 2x\left( {2x – 3} \right) + y\left( {y – 3} \right) + 2xy\).
Tìm giá trị lớn nhất của \(P = \frac{{6x + 2y + 1}}{{2x + y + 6}}\).
A. \(2\).

B. \(1\).

C. \(3\).

D. \(4\).

Lời giải chi tiết

PHÁT TRIỂN TƯƠNG TỰ CÂU 47 ĐỀ TOÁN THAM KHẢO 2021 CỦA BỘ.
BIÊN SOẠN TỪ STRONG TEAM TOÁN VDC – BIÊN TẬP WEB BOOKTOAN.COM

Ta có \({\log _{\sqrt 3 }}\frac{{2x + y}}{{4{x^2} + {y^2} + 2xy + 2}} = 2x\left( {2x – 3} \right) + y\left( {y – 3} \right) + 2xy\)
\( \Leftrightarrow {\log _{\sqrt 3 }}\left( {2x + y} \right) + 3\left( {2x + y} \right) + 2 = {\log _{\sqrt 3 }}\left( {4{x^2} + {y^2} + 2xy + 2} \right) + \left( {4{x^2} + {y^2} + 2xy + 2} \right)\)
\( \Leftrightarrow {\log _{\sqrt 3 }}\left( {2x + y} \right) + 3\left( {2x + y} \right) + {\log _{\sqrt 3 }}3 = {\log _{\sqrt 3 }}\left( {4{x^2} + {y^2} + 2xy + 2} \right) + \left( {4{x^2} + {y^2} + 2xy + 2} \right)\)
\( \Leftrightarrow {\log _{\sqrt 3 }}\left[ {3\left( {2x + y} \right)} \right] + 3\left( {2x + y} \right) = {\log _{\sqrt 3 }}\left( {4{x^2} + {y^2} + 2xy + 2} \right) + \left( {4{x^2} + {y^2} + 2xy + 2} \right)\) \(\left( * \right)\).
Xét hàm số \(f\left( t \right) = {\log _{\sqrt 3 }}t + t\), với \(t > 0\) có \(f’\left( t \right) = \frac{1}{{t.\ln \sqrt 3 }} + 1 > 0\), \(\forall t > 0\).
Vậy hàm số \(f\left( t \right)\) liên tục và đồng biến trên khoảng \(\left( {0; + \infty } \right)\).
Do đó: \(f\left( {3\left( {2x + y} \right)} \right) = f\left( {4{x^2} + {y^2} + 2xy + 2} \right) \Leftrightarrow 3\left( {2x + y} \right) = 4{x^2} + {y^2} + 2xy + 2\) \(\left( 1 \right)\).
Từ \(\left( 1 \right)\) \( \Leftrightarrow 2xy = {\left( {2x + y} \right)^2} – 3\left( {2x + y} \right) + 2\).
Ta có \(2x = 2x + 2xy – 2xy = 2x\left( {y + 1} \right) – 2xy \le {\left( {\frac{{2x + y + 1}}{2}} \right)^2} – 2xy\).
Đẳng thức xảy ra khi và chỉ khi \(2x = y + 1\).
Do đó từ \(\left( 1 \right)\), suy ra: \(2x \le \frac{{{{\left( {2x + y + 1} \right)}^2}}}{4} – {\left( {2x + y} \right)^2} + 3\left( {2x + y} \right) – 2\).
Đặt \(t = 2x + y\), \(t > 0\).
Suy ra: \(P = \frac{{2\left( {2x + y} \right) + 1 + 2x}}{{2x + y + 6}} \le \frac{{2t + 1 + \frac{{{{\left( {t + 1} \right)}^2}}}{4} – {t^2} + 3t – 2}}{{t + 6}} = \frac{{ – 3{t^2} + 22t – 3}}{{4\left( {t + 6} \right)}} = f\left( t \right)\).
Ta có: \(f’\left( t \right) = \frac{{ – 3{t^2} – 36t + 135}}{{4{{\left( {t + 6} \right)}^2}}} = 0 \Leftrightarrow t = 3\) (nhận).
Bảng biến thiên

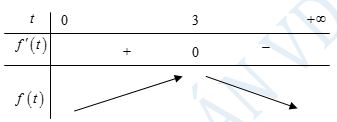
Dựa vào BBT, ta có \(\max P = \mathop {\max }\limits_{\left( {0; + \infty } \right)} f\left( t \right) = f\left( 3 \right) = 1\) khi và chỉ khi \(\left\{ \begin{array}{l}2x = y + 1\\2x + y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\).