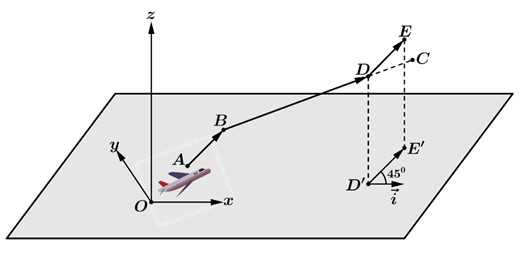
Trong không gian với hệ trục tọa độ $Oxyz$ (Đơn vị đo trên mỗi trục tọa độ dài 1 km, mặt đất là mặt phẳng $Oxy$). Lúc đó, một chiếc máy bay bắt đầu di chuyển từ điểm $A\left(700;850;100\right)$ với vận tốc không đổi $150$ (km/h) theo hướng về điểm $B\left(800;900;200\right)$. Khi tới $B$, máy bay thay đổi hướng bay theo hướng về điểm $C\left(1100;1400;300\right)$ với vận tốc giữ nguyên là $150$ (km/h). Máy bay di chuyển theo hướng mới trong $30\sqrt{35}$ phút (tức là mới tới điểm $D\in BC$) thì bất ngờ gặp gió lớn khiến hướng bay của nó lệch đi $45^\circ$ theo phương nằm ngang (tức là nếu $\overrightarrow{u}$ là vectơ hình chiếu xuống mặt đất của đoạn đường từ điểm $D$ trở đi thì góc lượng giác $\left(\overrightarrow{\imath};\overrightarrow{u}\right)=45^\circ$) và vận tốc giảm còn $120$ (km/h). Máy bay tiếp tục bay theo hướng lệch trong 30 phút.
a) Tổng thời gian bay thực tế của máy bay trong cả hành trình này là 142 phút (Kết quả làm tròn đến hàng đơn vị)
b) Khi bắt đầu gặp gió lớn, máy bay cách mặt đất 275km
c) Gọi $E\left(a;b;c\right)$ là vị trí cuối cùng của máy bay trong hành trình này. Khi đó $a+b+c=$ 2670 (Kết quả làm tròn đến hàng đơn vị)
d) Tổng quãng đường cả hành trình dài hơn 650 km
Lời giải: Sai: Ta có $AB=\sqrt{100^2+50^2+100^2}=150$ km
Thời gian bay từ $A$ đến $B$ là: $t_{A\to B}=\dfrac{150}{150}=1$ giờ
Thời gian bay từ $B$ đến $D$ là $30\sqrt{35}$ phút; thời gian bay từ $D$ đến $E$ là $30$ phút
Vậy tổng thời gian bay thực tế trong cả hành trình là: $\sum{t}=60+30\sqrt{35}+30\approx 267$ phút.
Đúng: Ta có $\overrightarrow{v_{BD}}\parallel\overrightarrow{BC}$ nên $\overrightarrow{v_{BD}}=\left|\overrightarrow{v_{BD}}\right|.\dfrac{\overrightarrow{BC}}{BC}=150.\dfrac{\left(300;500;100\right)}{\sqrt{300^2+500^2+100^2}}=100.\dfrac{\left(3;5;1\right)}{\sqrt{35}}$
Mặt khác $30\sqrt{35}$ phút$=\dfrac{\sqrt{35}}{2}$ giờ và $\overrightarrow{BD}=t_{B\to D}.\overrightarrow{v_{BD}}=\dfrac{\sqrt{35}}{2}.\dfrac{150}{\sqrt{35}}.\left(3;5;1\right)=\left(225;375;75\right)$
Khi đó tọa độ điểm $D=B+\left(225;375;75\right)=\left(1025;1275;275\right)$
Vậy $z_D=275$ nên khi bắt đầu gặp gió lớn, máy bay cách mặt đất 275km.
Sai:
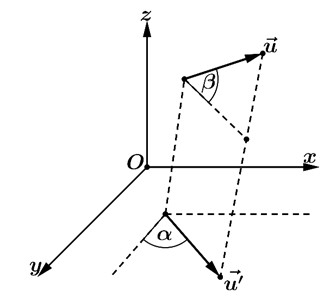
Ta có: $x_{\overrightarrow{u}}=\left|\overrightarrow{u’}\right|.\cos\alpha=\left|\overrightarrow{u}\right|.\cos\beta.\cos\alpha ;y_{\overrightarrow{u}}=\left|\overrightarrow{u’}\right|.\sin\alpha=\left|\overrightarrow{u}\right|.\cos\beta.\sin\alpha ;z_{\overrightarrow{u}}=\left|\overrightarrow{u}\right|.\sin\beta$
Áp dụng: $\beta=\left(DE;\left(Oxy\right)\right)=\left(DC;\left(Oxy\right)\right)=\left(BC;\left(Oxy\right)\right)$ mà $\overrightarrow{BC}\parallel\left(3;5;1\right)$ và $\overrightarrow{n_{\left(Oxy\right)}}=\left(0;0;1\right)$
Suy ra $\sin\beta=\dfrac{1}{\sqrt{35}.1}=\dfrac{1}{\sqrt{35}}\Rightarrow\cos\beta=\sqrt{\dfrac{34}{35}}$
Vậy $\left\{\begin{array}{l} {x_{\overrightarrow{v’}}}=\left|\overrightarrow{v’}\right|.\cos\beta.\cos\alpha=120.\sqrt{\dfrac{34}{35}}.\cos 45^\circ\simeq 83,63\\ {y_{\overrightarrow{v’}}}=\left|\overrightarrow{v’}\right|.\cos\beta.\sin\alpha=120.\sqrt{\dfrac{34}{35}}.\sin 45^\circ\simeq 83,63.\\ {z_{\overrightarrow{v’}}}=\left|\overrightarrow{v’}\right|.\sin\beta=120.\dfrac{1}{\sqrt{35}}\simeq 20,28\end{array}\right.$
Suy ra $\overrightarrow{DE}=t_{D\to E}.\overrightarrow{v’}=\dfrac{1}{2}.\overrightarrow{v’}\Rightarrow\overrightarrow{OE}=\overrightarrow{OD}+\dfrac{1}{2}\overrightarrow{v’}=\left(1025;1275;275\right)+\dfrac{1}{2}\overrightarrow{v}$
Vậy $a+b+c=\left(1025+\dfrac{1}{2}.83,63\right)+\left(1275+\dfrac{1}{2}.83,63\right)+\left(275+\dfrac{1}{2}.20,28\right)\approx 2669$
Đúng: Tổng quãng đường máy bay di chuyển trong cả hành trình là:
$S=AB+BD+DE=150+75\sqrt{35}+120.\dfrac{1}{2}\approx 653,7{>}650$ km.
(Sai) Tổng thời gian bay thực tế của máy bay trong cả hành trình này là 142 phút (Kết quả làm tròn đến hàng đơn vị)
(Sai) Khi bắt đầu gặp gió lớn, máy bay cách mặt đất 275km
(Sai) Gọi $E\left(a;b;c\right)$ là vị trí cuối cùng của máy bay trong hành trình này. Khi đó $a+b+c=$ 2670 (Kết quả làm tròn đến hàng đơn vị)
(Sai) Tổng quãng đường cả hành trình dài hơn 650 km
(Sai) Tổng thời gian bay thực tế của máy bay trong cả hành trình này là 142 phút (Kết quả làm tròn đến hàng đơn vị)
(Sai) Khi bắt đầu gặp gió lớn, máy bay cách mặt đất 275km
(Sai) Gọi $E\left(a;b;c\right)$ là vị trí cuối cùng của máy bay trong hành trình này. Khi đó $a+b+c=$ 2670 (Kết quả làm tròn đến hàng đơn vị)
(Sai) Tổng quãng đường cả hành trình dài hơn 650 km
