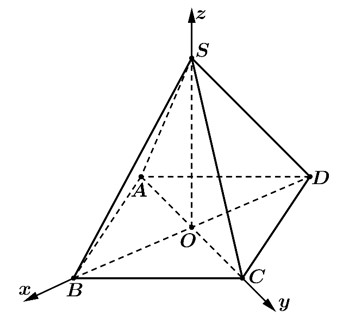
Trong không gian với hệ trục tọa độ $Oxyz$, cho hình chóp đều $S.ABCD$ với đáy $ABCD$ là hình vuông cạnh bằng $2\sqrt{2}$ và cạnh bên $SA=4$. Gọi $O$ là tâm của hình vuông $ABCD$ (Minh họa như hình vẽ dưới đây)
a) Tọa độ của điểm $A\left( 0;2;0 \right)$
b) Trọng tâm của tam giác $SAB$ là $G\left( \dfrac{2}{3};-\dfrac{2}{3};\dfrac{2\sqrt{3}}{3} \right)$
c) Nếu điểm $E\left( a;0;b \right)$ là một điểm thuộc mặt phẳng $\left( Oxz \right)$ sao cho ba điểm $C,E,G$ thẳng hàng thì tích $a.b=\sqrt{3}$
d) Nếu điểm $M\left( 0;m;n \right)$ thuộc mặt phẳng $\left( Oyz \right)$ sao cho $MG+MB$ đạt giá trị nhỏ nhất thì giá trị của biểu thức $T={{m}^{2}}+{{n}^{2}}=1$
Lời giải:
(Sai) Tọa độ của điểm $A\left( 0;2;0 \right)$
(Vì): Sai: Tọa độ của điểm $A\left( 0;-2;0 \right)$
(Đúng) Trọng tâm của tam giác $SAB$ là $G\left( \dfrac{2}{3};-\dfrac{2}{3};\dfrac{2\sqrt{3}}{3} \right)$
(Vì): Đúng: Ta có $A\left( 0;-2;0 \right)$; $B\left( 0;2;0 \right)$; $C\left( 0;0;2\sqrt{3} \right)$ nên tọa độ trong tâm $G\left( \dfrac{2}{3};-\dfrac{2}{3};\dfrac{2\sqrt{3}}{3} \right)$
(Sai) Nếu điểm $E\left( a;0;b \right)$ là một điểm thuộc mặt phẳng $\left( Oxz \right)$ sao cho ba điểm $C,E,G$ thẳng hàng thì tích $a.b=\sqrt{3}$
(Vì): Sai: $C$ là điểm đối xứng với $A$ qua gốc tọa độ $O$ nên $C\left( 0;2;0 \right)$ Khi đó: $\overrightarrow{CE}=\left( a;-2;b \right)$ và $\overrightarrow{CG}=\left( \dfrac{2}{3};-\dfrac{8}{3};\dfrac{2\sqrt{3}}{3} \right)\parallel \left( 1;-4;\sqrt{3} \right)$ và điều kiện cùng phương là: $\dfrac{a}{1}=\dfrac{-2}{-4}=\dfrac{b}{\sqrt{3}}$ $\Rightarrow a=\dfrac{1}{2};b=\dfrac{\sqrt{3}}{2}$ nên $a.b=\dfrac{\sqrt{3}}{4}$
(Đúng) Nếu điểm $M\left( 0;m;n \right)$ thuộc mặt phẳng $\left( Oyz \right)$ sao cho $MG+MB$ đạt giá trị nhỏ nhất thì giá trị của biểu thức $T={{m}^{2}}+{{n}^{2}}=1$
(Vì): Đúng: Gọi ${B}’$ là điểm đối xứng với $B$ qua mặt phẳng $\left( Oyz \right)$ thì ${B}’\left( -2;0;0 \right)$ Đường thẳng $G{B}’$ có một vectơ chỉ phương là $\overrightarrow{G{B}’}=\left( -\dfrac{8}{3};\dfrac{2}{3};-\dfrac{2\sqrt{3}}{3} \right)\parallel \left( 4;-1;\sqrt{3} \right)$ Phương trình đường thẳng $G{B}’$ là: $\left\{ \begin{array}{l} x=\dfrac{2}{3}+4t \\ y=-\dfrac{2}{3}-t \\ z=\dfrac{2\sqrt{3}}{3}+\sqrt{3}t \end{array} \right.$ Giao điểm của $M$ với mặt phẳng $\left( Oyz \right)$ tức là $x=0\Leftrightarrow \dfrac{2}{3}+4t=0\Leftrightarrow t=-\dfrac{1}{6}$ thay vào đường thẳng $G{B}’$ ta được: $m=y=-\dfrac{1}{2}$ và $n=z=\dfrac{\sqrt{3}}{2}$. Do vậy $T={{m}^{2}}+{{n}^{2}}={{\left( -\dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}=1$.
(Sai) Tọa độ của điểm $A\left( 0;2;0 \right)$
(Đúng) Trọng tâm của tam giác $SAB$ là $G\left( \dfrac{2}{3};-\dfrac{2}{3};\dfrac{2\sqrt{3}}{3} \right)$
(Sai) Nếu điểm $E\left( a;0;b \right)$ là một điểm thuộc mặt phẳng $\left( Oxz \right)$ sao cho ba điểm $C,E,G$ thẳng hàng thì tích $a.b=\sqrt{3}$
(Đúng) Nếu điểm $M\left( 0;m;n \right)$ thuộc mặt phẳng $\left( Oyz \right)$ sao cho $MG+MB$ đạt giá trị nhỏ nhất thì giá trị của biểu thức $T={{m}^{2}}+{{n}^{2}}=1$
