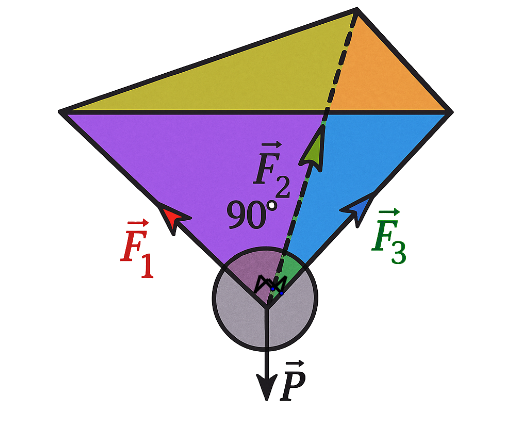
Treo một vật nặng có trọng lượng 30 N bởi ba sợi dây giống hệt nhau, các sợi dây đôi một tạo với nhau một góc ${90^{\circ}}$ như Hình. Gọi ${\overrightarrow{F_1}, \overrightarrow{F_2}, \overrightarrow{F_3}}$ lần lượt là các lực căng của ba sợi dây nói trên. Độ lớn của lực ${\vec{F}_1}$ bằng bao nhiêu Niutơn? (Làm tròn kết quả đến hàng đơn vị)
Lời giải
Đáp số: 52
Xét tứ diện đều ${S A B C}$ có các cạnh ${S A, S B, S C}$ biểu diễn độ lớn các lực căng dây và ${S P}$ biểu diễn độ lớn của trọng lực tác dụng lên vật nặng ${S}$.
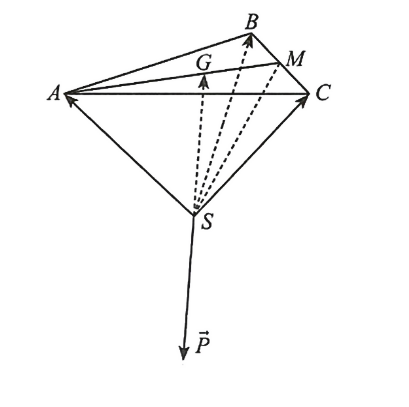
Tacó ${\left|\vec{F}_1\right|=S A,\left|\vec{F}_2\right|=S B,\left|\overrightarrow{F_3}\right|=S C,|\vec{P}|=S G}$ và ${\overrightarrow{S G}+\overrightarrow{S P}=\overrightarrow{0}}$, trong đó ${G}$ là trọng tâm của tam giác đều ${A B C}$.
Đặt ${x=S A, x{>}0 \Rightarrow A C=x \sqrt{2}}$.
Khi đó ${A G=\dfrac{2}{3} A M=\dfrac{2}{3}\left(\dfrac{A C \sqrt{3}}{2}\right)=\dfrac{x \sqrt{6}}{3}}$.
Mặt khác ${S G=S P=30}$ nên xét tam giác ${S A G}$ vuông tại ${G}$, ta có
$S{{A}^{2}}=S{{G}^{2}}+A{{G}^{2}}\Leftrightarrow {{x}^{2}}={{30}^{2}}+\dfrac{2{{x}^{2}}}{3}\Leftrightarrow x=30\sqrt{3}\approx 52(N)\text{. }$
