Trắc nghiệm Ứng dụng Tích phân

Cho hàm số \(f\left( x \right)\) có đạo hàm cấp hai liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( 0 \right) = f'\left( 0 \right) = 0,\,f''\left( x \right) - \left( {2x + 1} \right){e^x} = f\left( x \right)\) với mọi \(x \in \mathbb{R}\). Giá trị của \(f\left( 2 \right)\) bằng A. \({e^2}\). B. \(2{e^4}\). C. \(2{e^2}\). D. \({e^4}\). Lời giải Ta có: … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) có đạo hàm cấp hai liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( 0 \right) = f’\left( 0 \right) = 0,\,f”\left( x \right) – \left( {2x + 1} \right){e^x} = f\left( x \right)\) với mọi \(x \in \mathbb{R}\). Giá trị của \(f\left( 2 \right)\) bằng

  Cho hàm số \(f(x)\) thỏa mãn:\(3f( - x) - 2f(x) = {\tan ^2}x\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), trục tung và đường thẳng \(x = \frac{\pi }{4}\). A. \(\frac{{{\pi ^2}}}{{12}}\). B. \(\frac{\pi }{{12}}\). C. \(\frac{\pi }{2}\). D. \(\frac{{{\pi ^2}}}{2}\). Lời … [Đọc thêm...] về  Cho hàm số \(f(x)\) thỏa mãn:\(3f( – x) – 2f(x) = {\tan ^2}x\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), trục tung và đường thẳng \(x = \frac{\pi }{4}\).

Cho hàm số \(f\left( x \right)\) liên tục không âm trên \(\left[ {0\,;\frac{\pi }{2}} \right]\), thỏa mãn \(f\left( x \right).f'\left( x \right) = \cos x.\sqrt {1 + {f^2}\left( x \right)} \) với mọi \(x \in \left[ {0\,;\frac{\pi }{2}} \right]\) và \(f\left( 0 \right) = 2\sqrt 2 \). Giá trị của \(f\left( {\frac{\pi }{2}} \right)\) bằng A. \(2\). B. \(2\sqrt 2 \). C. … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục không âm trên \(\left[ {0\,;\frac{\pi }{2}} \right]\), thỏa mãn \(f\left( x \right).f’\left( x \right) = \cos x.\sqrt {1 + {f^2}\left( x \right)} \) với mọi \(x \in \left[ {0\,;\frac{\pi }{2}} \right]\) và \(f\left( 0 \right) = 2\sqrt 2 \). Giá trị của \(f\left( {\frac{\pi }{2}} \right)\) bằng

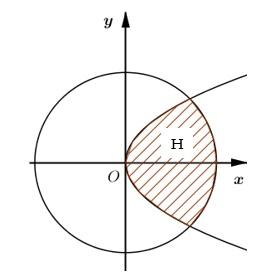
  Cho hình \(H\) giới hạn bởi các đường \({y^2} = 2x\) và \({x^2} + {y^2} = 8\)( phần gạch sọc trong hình). Khối tròn xoay khi quay \(H\) xung quanh trục \(Ox\) có thể tích bằng bao nhiêu? A. \(\frac{{2\pi \left( {8\sqrt 2  - 7} \right)}}{3}\). B. \(\frac{{4\pi \left( {13 - 8\sqrt 2 } \right)}}{3}\). C. \(\left( {\frac{{32\sqrt 2 }}{3} - 8} \right)\pi … [Đọc thêm...] về  Cho hình \(H\) giới hạn bởi các đường \({y^2} = 2x\) và \({x^2} + {y^2} = 8\)( phần gạch sọc trong hình). Khối tròn xoay khi quay \(H\) xung quanh trục \(Ox\) có thể tích bằng bao nhiêu?

Cho \(f\left( x \right)\) là hàm liên tục trên \(\mathbb{R}\). Với số thực \(a > 0\), giả sử rằng mọi \(x \in \left[ {0;a} \right]\) ta có \(f\left( x \right) > 0\) và \(f\left( x \right)f\left( {a - x} \right) = 1\). Tính \(I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}{\rm{d}}x} \). A. \(\frac{a}{3}\). B. \(2a\). C. \(a\ln \left( {1 + a} … [Đọc thêm...] vềCho \(f\left( x \right)\) là hàm liên tục trên \(\mathbb{R}\). Với số thực \(a > 0\), giả sử rằng mọi \(x \in \left[ {0;a} \right]\) ta có \(f\left( x \right) > 0\) và \(f\left( x \right)f\left( {a – x} \right) = 1\). Tính \(I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}{\rm{d}}x} \).

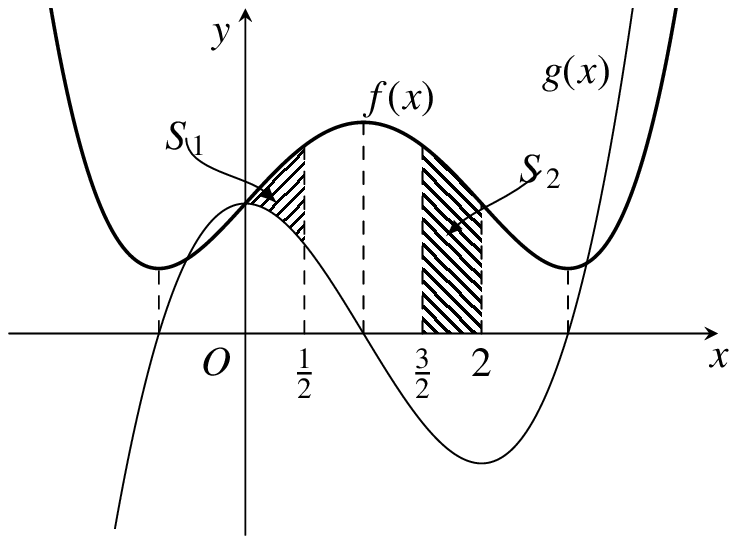
Cho hàm số \(f(x) = a{x^4} - {x^3} + 2x + 2\) và hàm số \(g(x) = b{x^3} + c{x^2} + 2\), có đồ thị như hình vẽ bên. Gọi \({S_1};{S_2}\) là diện tích các hình phẳng gạch chéo trong hình vẽ, biết \({S_2} = \frac{{791}}{{640}}\). Khi đó \({S_1}\) bằng A. \(\frac{{231}}{{640}}\). B. \(\frac{{271}}{{320}}\). C. \(\frac{{571}}{{640}}\). D. … [Đọc thêm...] vềCho hàm số \(f(x) = a{x^4} – {x^3} + 2x + 2\) và hàm số \(g(x) = b{x^3} + c{x^2} + 2\), có đồ thị như hình vẽ bên. Gọi \({S_1};{S_2}\) là diện tích các hình phẳng gạch chéo trong hình vẽ, biết \({S_2} = \frac{{791}}{{640}}\). Khi đó \({S_1}\) bằng

Cho hàm số \(f\left( x \right)\) liên tục và luôn nhận giá trị dương trên khoảng \(\left( {2;4} \right)\), thỏa mãn \(f\left( 3 \right) = \frac{1}{{{e^2}}}\) và \({f^3}\left( x \right) + {e^{ - 2x}} = 3{e^{ - x}}\sqrt {f\left( x \right)} .f'\left( x \right),\;\;\forall x \in \left( {2;4} \right)\). Khi đó \(f\left( {\frac{5}{2}} \right)\) thuộc khoảng A. \(\left( {1;2} … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục và luôn nhận giá trị dương trên khoảng \(\left( {2;4} \right)\), thỏa mãn \(f\left( 3 \right) = \frac{1}{{{e^2}}}\) và \({f^3}\left( x \right) + {e^{ – 2x}} = 3{e^{ – x}}\sqrt {f\left( x \right)} .f’\left( x \right),\;\;\forall x \in \left( {2;4} \right)\). Khi đó \(f\left( {\frac{5}{2}} \right)\) thuộc khoảng

Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thoả mãn \(f'\left( x \right) - f\left( x \right) = \left( {2x + 3} \right){e^x}\) và \(f\left( 0 \right) = 5\) Tổng tất cả các nghiệm thực của phương trình \(f\left( x \right) = 3{e^x}\) bằng A. \(2\). B. \( - 3\). C. \(1\). D. \(3\). Lời giải Ta có \(f'\left( x \right) - f\left( x … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) thoả mãn \(f’\left( x \right) – f\left( x \right) = \left( {2x + 3} \right){e^x}\) và \(f\left( 0 \right) = 5\) Tổng tất cả các nghiệm thực của phương trình \(f\left( x \right) = 3{e^x}\) bằng

  Một sân chơi dành riêng cho trẻ em hình chữ nhật có chiều dài 50m và chiều rộng 30m, người ta làm một con đường trong sân (như hình vẽ). Biết viền ngoài và viền trong của con đường là hai đường elip và chiều rộng của mặt đường là 2m. Kinh phí để làm mỗi \({m^2}\) làm đường 500.000 đồng. Tính tổng số tiền làm con đường đó (số tiền làm tròn đến hàng nghìn). A. … [Đọc thêm...] về  Một sân chơi dành riêng cho trẻ em hình chữ nhật có chiều dài 50m và chiều rộng 30m, người ta làm một con đường trong sân (như hình vẽ). Biết viền ngoài và viền trong của con đường là hai đường elip và chiều rộng của mặt đường là 2m. Kinh phí để làm mỗi \({m^2}\) làm đường 500.000 đồng. Tính tổng số tiền làm con đường đó (số tiền làm tròn đến hàng nghìn).

Cho hàm số \(f(x)\) xác định trên \(\mathbb{R}\backslash \left\{ {\frac{1}{3}} \right\}\), có đạo hàm thỏa mãn \(f'\left( x \right) = \frac{3}{{3x - 1}},\forall x \in \mathbb{R}\backslash \left\{ {\frac{1}{3}} \right\}\) và \(f\left( 0 \right) = 2024\), \(f\left( {\frac{2}{3}} \right) = 2025\). Giá trị của biểu thức \(f\left( { - 1} \right) + f\left( 3 \right)\) bằng A. … [Đọc thêm...] vềCho hàm số \(f(x)\) xác định trên \(\mathbb{R}\backslash \left\{ {\frac{1}{3}} \right\}\), có đạo hàm thỏa mãn \(f’\left( x \right) = \frac{3}{{3x – 1}},\forall x \in \mathbb{R}\backslash \left\{ {\frac{1}{3}} \right\}\) và \(f\left( 0 \right) = 2024\), \(f\left( {\frac{2}{3}} \right) = 2025\). Giá trị của biểu thức \(f\left( { – 1} \right) + f\left( 3 \right)\) bằng