Trắc nghiệm Ứng dụng Tích phân

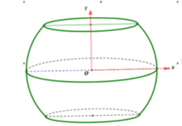
  Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được. A. \(\frac{{100}}{3}\pi \left( {d{m^3}} \right)\). B. \(\frac{{43}}{3}\pi \left( … [Đọc thêm...] về  Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước (như hình vẽ). Tính thể tích mà chiếc lu chứa được.

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\) A. \(\frac{5}{4}\). B. \(\frac{3}{2}\). C. \(\frac{1}{2}\). D. \(2\). Lời giải Đặt: \(y = f\left( x \right) \Rightarrow x = {y^3} + y.\) \( \Rightarrow dx = … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \({f^3}\left( x \right) + f\left( x \right) = x,\)\(\forall x \in \mathbb{R}.\)Tính \(\int\limits_0^2 {f\left( x \right)} dx.\)

  Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) - f'\left( x \right) = 3x\left( {2x - 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) =  - 1\). Giá trị của \(f\left( 2 \right)\) bằng A. \(7\). B. \(6\). C. \(1\). D. \(2\). Lời giải Ta có: \(2f\left( x \right) - f'\left( x … [Đọc thêm...] về  Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(2f\left( x \right) – f’\left( x \right) = 3x\left( {2x – 5} \right)\), \(\forall x \in \mathbb{R}\). Biết rằng \(f\left( 0 \right) =  – 1\). Giá trị của \(f\left( 2 \right)\) bằng

  Cho hàm số \(f(x)\) liên tục với mọi \(x \ne 0\) thỏa mãn:\(f(x) + 2f\left( {\frac{1}{x}} \right) = 3x\) với \(x \ne 0\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), và hai đường thẳng \(x = 1;\,x = 2\). A. \(\frac{{{\pi ^2}}}{{12}}\). B. \(\frac{\pi }{3}\). C. \(\frac{\pi … [Đọc thêm...] về  Cho hàm số \(f(x)\) liên tục với mọi \(x \ne 0\) thỏa mãn:\(f(x) + 2f\left( {\frac{1}{x}} \right) = 3x\) với \(x \ne 0\). Tính thể tích vật thể tròn xoay khi quay quanh \(Ox\) bởi hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục \(Ox\), và hai đường thẳng \(x = 1;\,x = 2\).

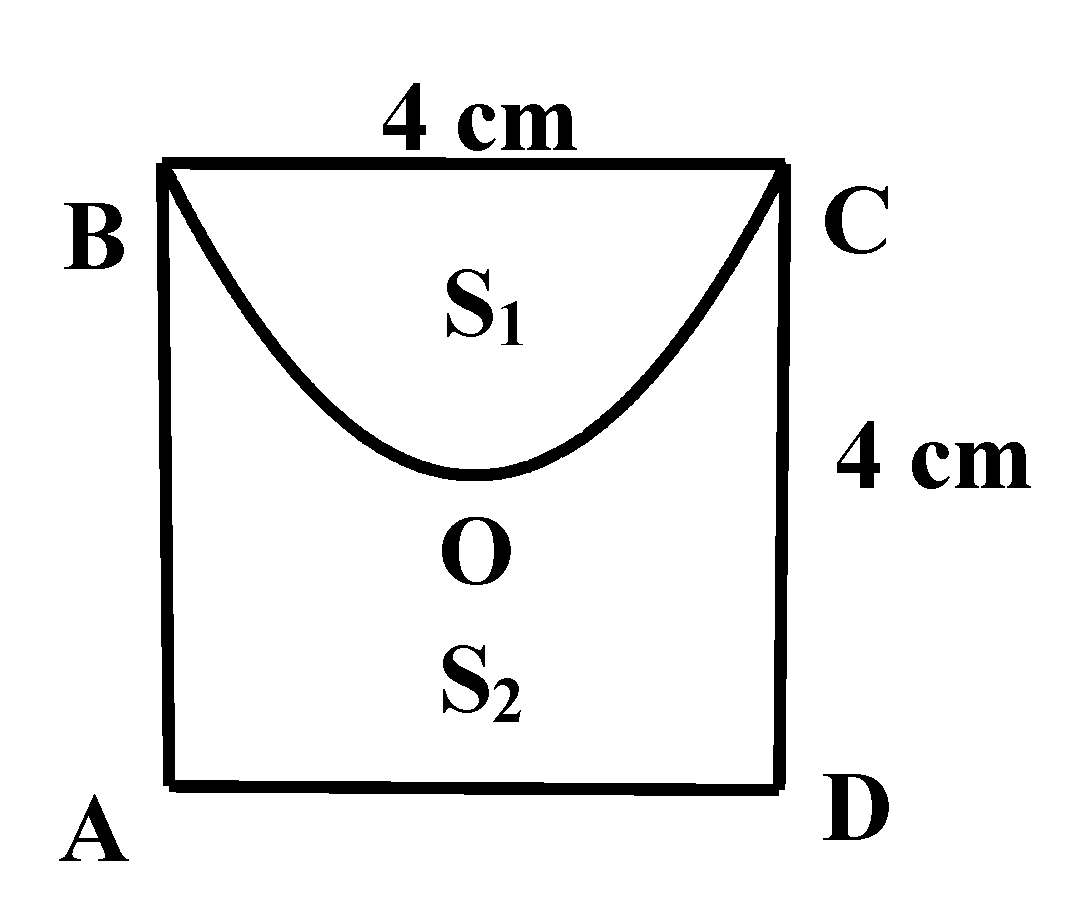
  Cho hình vuông \(ABCD\) tâm\(O\), độ dài cạnh là \(4\) cm. Đường cong \(BOC\) là một phần của parabol đỉnh \(O\) chia hình vuông thành hai hình phẳng có diện tích lần lượt là \({S_1}\) và \({S_2}\) (tham khảo hình vẽ). Tỉ số \(\frac{{{S_1}}}{{{S_2}}}\) bằng A. \(\frac{2}{5}\). B. \(\frac{1}{2}\). C. \(\frac{1}{3}\). D. \(\frac{3}{5}\). Lời … [Đọc thêm...] về  Cho hình vuông \(ABCD\) tâm\(O\), độ dài cạnh là \(4\) cm. Đường cong \(BOC\) là một phần của parabol đỉnh \(O\) chia hình vuông thành hai hình phẳng có diện tích lần lượt là \({S_1}\) và \({S_2}\) (tham khảo hình vẽ).

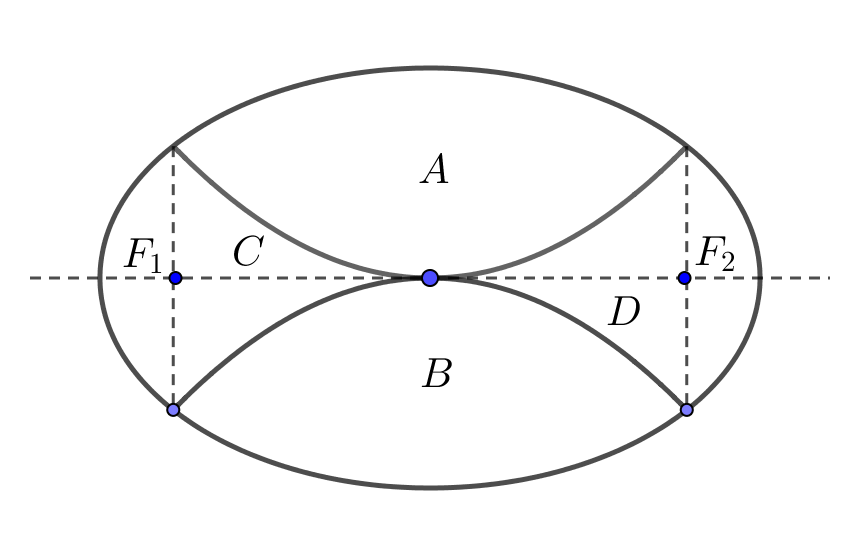
Nhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là \(8{\rm{ m}}\) và \({\rm{4 m}}\); \({F_1}\), \({F_2}\) lần lượt là hai tiêu điểm của elip. Phần \(A\), \(B\) dùng để trồng hoa, phần \(C\), \(D\) dùng để trồng cỏ. … [Đọc thêm...] vềNhà trường dự định làm một vườn hoa dạng hình elip được chia ra làm bốn phần bởi hai đường parabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là \(8{\rm{ m}}\) và \({\rm{4 m}}\); \({F_1}\), \({F_2}\) lần lượt là hai tiêu điểm của elip. Phần \(A\), \(B\) dùng để trồng hoa, phần \(C\), \(D\) dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là \(270.000\) đ và \(140.{\rm{000}}\) đ. Tính tổng số tiền để hoàn thành vườn hoa trên (làm tròn đến hàng nghìn).

  Cho hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\) nằm phía trên trục hoành. Hàm số \(y = f\left( x \right)\) thỏa mãn các điều kiện \({\left[ {f'\left( x \right)} \right]^2} + f''\left( x \right).f\left( x \right) + 4 = 0,\,\,f\left( 0 \right) = 0,\,\,f\left( {\frac{1}{2}} \right) = \sqrt 3 .\) Tính \(f\left( 1 \right)\). A. \(20\). B. … [Đọc thêm...] về  Cho hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\) nằm phía trên trục hoành. Hàm số \(y = f\left( x \right)\) thỏa mãn các điều kiện \({\left[ {f’\left( x \right)} \right]^2} + f”\left( x \right).f\left( x \right) + 4 = 0,\,\,f\left( 0 \right) = 0,\,\,f\left( {\frac{1}{2}} \right) = \sqrt 3 .\) Tính \(f\left( 1 \right)\).

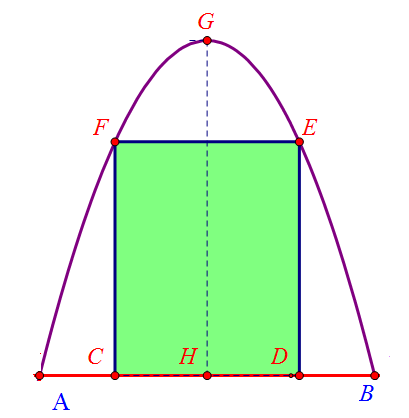
Một cái cổng hình Parabol như hình vẽ sau. Chiều cao \(GH = 4m\), chiều rộng \(AB = 4m\), \(AC = BD = 0,9m\). Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1200000\) đồng\(/{m^2}\), còn các phần để trắng làm xiên hoa có giá là \(900000\) đồng\(/{m^2}\). Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây? A. … [Đọc thêm...] vềMột cái cổng hình Parabol như hình vẽ sau. Chiều cao \(GH = 4m\), chiều rộng \(AB = 4m\), \(AC = BD = 0,9m\). Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1200000\) đồng\(/{m^2}\), còn các phần để trắng làm xiên hoa có giá là \(900000\) đồng\(/{m^2}\). Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?