Trắc nghiệm Ứng dụng Tích phân

(Sở Bắc Giang 2022) Cho hàm số \(f(x) = \left\{ {\begin{array}{{20}{l}}{{e^x} + m}&{{\rm{ khi }}}&{x \ge 0}\\{{x^2}{{\left( {{x^3} + 1} \right)}^3}}&{{\rm{ khi }}}&{x < 0}\end{array}} \right.\) (với m là tham số). Biết hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và \(\int_{ – 1}^1 f (x)dx = a \cdot e – \frac{b}{c}\) với \(a,b,c \in {\mathbb{N}^};\frac{b}{c}\) tối giản \((e = 2,718281828)\). Biểu thức \(a + b + c + m\) bằng

Câu hỏi: (Sở Bắc Giang 2022) Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{e^x} + m}&{{\rm{ khi }}}&{x \ge 0}\\{{x^2}{{\left( {{x^3} + 1} \right)}^3}}&{{\rm{ khi }}}&{x < 0}\end{array}} \right.\) (với m là tham số). Biết hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và \(\int_{ - 1}^1 f (x)dx = a \cdot e - \frac{b}{c}\) với \(a,b,c \in … [Đọc thêm...] về

(Sở Bắc Giang 2022) Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{{e^x} + m}&{{\rm{ khi }}}&{x \ge 0}\\{{x^2}{{\left( {{x^3} + 1} \right)}^3}}&{{\rm{ khi }}}&{x < 0}\end{array}} \right.\) (với m là tham số). Biết hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và \(\int_{ – 1}^1 f (x)dx = a \cdot e – \frac{b}{c}\) với \(a,b,c \in {\mathbb{N}^*};\frac{b}{c}\) tối giản \((e = 2,718281828)\). Biểu thức \(a + b + c + m\) bằng

Cho hàm số \(y = f\left( x \right) = 6{x^4} + a{x^3} + b{x^2} + cx + d\quad \left( {a,b,c,d \in \mathbb{R}} \right)\). Biết đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị có hoành độ lần lượt là \( – 1;\;1;2\) và hàm số \(y = g\left( x \right)\)là hàm bậc hai có đồ thị đi ba điểm cực trị đó . Tính diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\); \(y = g\left( x \right)\)và trục \(Oy\).

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(y = f\left( x \right) = 6{x^4} + a{x^3} + b{x^2} + cx + d\quad \left( {a,b,c,d \in \mathbb{R}} \right)\). Biết đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị có hoành độ lần lượt là \( - 1;\;1;2\) và hàm số \(y = g\left( x \right)\)là hàm bậc hai có đồ thị đi ba điểm cực trị đó . Tính diện tích hình phẳng giới hạn bởi các đường \(y = … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = 6{x^4} + a{x^3} + b{x^2} + cx + d\quad \left( {a,b,c,d \in \mathbb{R}} \right)\). Biết đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị có hoành độ lần lượt là \( – 1;\;1;2\) và hàm số \(y = g\left( x \right)\)là hàm bậc hai có đồ thị đi ba điểm cực trị đó . Tính diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\); \(y = g\left( x \right)\)và trục \(Oy\).

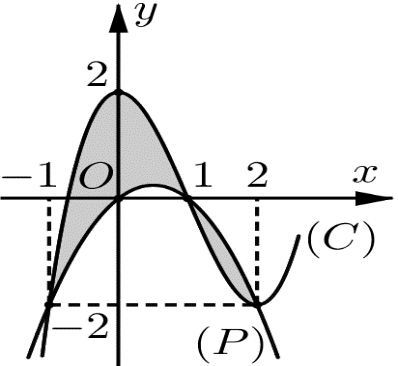
Hình phẳng được giới hạn bởi đồ thị \(\left( C \right)\) của hàm số đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Diện tích hình phẳng bằng

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Hình phẳng được giới hạn bởi đồ thị \(\left( C \right)\) của hàm số đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Diện tích hình phẳng bằng Lời Giải: Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG A. \(\frac{5}{{12}}\). B. \(\frac{7}{{12}}\). C. \(\frac{{11}}{{12}}\). D. … [Đọc thêm...] vềHình phẳng được giới hạn bởi đồ thị \(\left( C \right)\) của hàm số đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Diện tích hình phẳng bằng

Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\)có hai điểm cực tiểu \(\left( { – 1; – 2} \right);\left( {1; – 2} \right)\) và điểm cực đại \(\left( {0;3} \right)\). Hàm số\(y = g\left( x \right) = m{x^2} + nx + p\) có đồ thị đi qua các điểm cực trị của đồ thị \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\)và\(y = g\left( x \right)\)gần bằng giá trị nào nhất trong các giá trị sau

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có hai điểm cực tiểu \(\left( { - 1; - 2} \right);\left( {1; - 2} \right)\) và điểm cực đại \(\left( {0;3} \right)\). Hàm số\(y = g\left( x \right) = m{x^2} + nx + p\) có đồ thị đi qua các điểm cực trị của đồ thị \(y = f\left( x \right)\) . Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\)có hai điểm cực tiểu \(\left( { – 1; – 2} \right);\left( {1; – 2} \right)\) và điểm cực đại \(\left( {0;3} \right)\). Hàm số\(y = g\left( x \right) = m{x^2} + nx + p\) có đồ thị đi qua các điểm cực trị của đồ thị \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\)và\(y = g\left( x \right)\)gần bằng giá trị nào nhất trong các giá trị sau

Cho hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + d\,\left( {a,b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị \( – 1\,,\,0\,,\,1\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + d\,\left( {a,b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị \( - 1\,,\,0\,,\,1\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + d\,\left( {a,b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị \( – 1\,,\,0\,,\,1\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng

Cho hàm số \(f\left( x \right) = – {x^3} + b{x^2} + cx + d{\rm{ }}\left( {b,c,d \in \mathbb{R}} \right)\)có hai điểm cực trị là \( – 1\), \(\frac{5}{3}\) và có đồ thị cắt trục tung tại điểm có tung độ bằng \( – 2\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) và có đỉnh là \(I\left( {1;2} \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị thuộc khoảng nào sau đây

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(f\left( x \right) = - {x^3} + b{x^2} + cx + d{\rm{ }}\left( {b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị là \( - 1\), \(\frac{5}{3}\) và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 2\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) và có đỉnh … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = – {x^3} + b{x^2} + cx + d{\rm{ }}\left( {b,c,d \in \mathbb{R}} \right)\)có hai điểm cực trị là \( – 1\), \(\frac{5}{3}\) và có đồ thị cắt trục tung tại điểm có tung độ bằng \( – 2\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) và có đỉnh là \(I\left( {1;2} \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị thuộc khoảng nào sau đây

Mặt sàn của một thang máy có dạng hình vuông \(ABCD\) cạnh \(2{\rm{m}}\) được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ trục tọa độ \(Oxy\) với \(O\) là tâm hình vuông sao cho \(A\left( {1;1} \right)\) như hình vẽ bên thì các đường cong \(OA\) có phương trình \(y = {x^2}\) và \(y = a{x^3} + bx\). Tính giá trị \(a.b\) biết rằng diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\) diện tích mặt sàn.

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Mặt sàn của một thang máy có dạng hình vuông \(ABCD\) cạnh \(2{\rm{m}}\) được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ trục tọa độ \(Oxy\) với \(O\) là tâm hình vuông sao cho \(A\left( {1;1} \right)\) như hình vẽ bên thì các đường cong \(OA\) có phương trình \(y = {x^2}\) và \(y = a{x^3} + bx\). Tính giá trị \(a.b\) … [Đọc thêm...] vềMặt sàn của một thang máy có dạng hình vuông \(ABCD\) cạnh \(2{\rm{m}}\) được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ trục tọa độ \(Oxy\) với \(O\) là tâm hình vuông sao cho \(A\left( {1;1} \right)\) như hình vẽ bên thì các đường cong \(OA\) có phương trình \(y = {x^2}\) và \(y = a{x^3} + bx\). Tính giá trị \(a.b\) biết rằng diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\) diện tích mặt sàn.

Cho hàm số \(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có \(f\left( 0 \right) = 1\) và ba điểm cực trị là \(0;1;2.\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng đi qua điểm \(A\left( {3;10} \right)\) có hệ số góc bằng 4 bằng

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có \(f\left( 0 \right) = 1\) và ba điểm cực trị là \(0;1;2.\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng đi qua điểm \(A\left( {3;10} \right)\) có hệ số góc bằng 4 bằng Lời Giải: Đây là các câu trắc nghiệm về ứng … [Đọc thêm...] vềCho hàm số \(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có \(f\left( 0 \right) = 1\) và ba điểm cực trị là \(0;1;2.\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng đi qua điểm \(A\left( {3;10} \right)\) có hệ số góc bằng 4 bằng

Cho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( – \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = – 55\) .
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( - \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = - 55\) . Diện tích miền tô đậm gần số nào nhất trong các số sau đây? Lời Giải: Đây là các câu … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( – \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = – 55\) .

Diện tích miền tô đậm gần số nào nhất trong các số sau đây?

Cho hàm số \(y = f\left( x \right)\)là hàm đa thức bậc bốn và có đồ thị \((C)\) như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\,\)và \(y = f’\left( x \right)\)bằng \(\frac{{856}}{5}\). Tính diện tích hình phẳng giới hạn bởi đồ thị \((C)\) và parabol \((P)\) đi qua ba điểm cực trị của đồ thị \((C)\).

Ngày 09/06/2022 Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:Trắc nghiệm ứng dụng tích phân diện tích hình phẳng, VDC Toan 2022

Câu hỏi: Cho hàm số \(y = f\left( x \right)\)là hàm đa thức bậc bốn và có đồ thị \((C)\) như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\,\)và \(y = f'\left( x \right)\)bằng \(\frac{{856}}{5}\). Tính diện tích hình phẳng giới hạn bởi đồ thị \((C)\) và parabol \((P)\) đi qua ba điểm cực trị của đồ thị \((C)\). Lời Giải: … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\)là hàm đa thức bậc bốn và có đồ thị \((C)\) như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\,\)và \(y = f’\left( x \right)\)bằng \(\frac{{856}}{5}\). Tính diện tích hình phẳng giới hạn bởi đồ thị \((C)\) và parabol \((P)\) đi qua ba điểm cực trị của đồ thị \((C)\).