Trắc nghiệm Ứng dụng Tích phân

(THPT Nguyễn Tất Thành-Đh-SP-HN-2022) Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \ln x,\) trục hoành và hai đường thẳng \(x = 1;\;x = m,\) với \(m > 1.\) Khi hình phẳng \(D\) có diện tích bằng \(1,\) giá trị của \(m\) thuộc khoảng nào dưới đây ?

(Chuyên Lê Quý Đôn – Điện Biên – 2022) Xét hàm só́ \(f\left( x \right) = {e^x} + \int_0^1 x f\left( x \right){\rm{d}}x\). Giá trị của \(f\left( {\ln 2022} \right)\) bằng bao nhiêu?

(Đại học Hồng Đức – 2022) Cho hàm số \(f(x) = {x^3} + a{x^2} + bx + c(a,b,c \in \mathbb{R})\) có hai điểm cực trị là \( – 1\) và 1. Gọi \(y = g(x)\) là hàm số bậc hai có đồ thị cắt trục hoành tại hai điểm có hoành độ trùng với các điểm cực trị của \(f(x)\), đồng thời có đỉnh nằm trên đồ thị của \(f(x)\) với tung độ bằng 2. Diện tích hình phẳng giới hạn bởi hai đường \(y = f(x)\) và \(y = g(x)\) gần với giá trị nào nhất dưới đây?

(THPT Kim Liên – Hà Nội – 2022) Gọi \(S\) là diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} + 2x – 1\) và các đường thẳng \(y = m\), \(x = 0\), \(x = 1\). Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { – 4040; – 3} \right]\) để \(S \le 2021\)?

(THPT Hương Sơn – Hà Tĩnh – 2022) Cho hàm số \(y = f\left( x \right)\) liên tục, nhận giá trị dương trên \(\left( {0; + \infty } \right)\) và thỏa mãn \(f\left( 1 \right) = 2\); \(f’\left( x \right) = \frac{{{x^2}}}{{{{\left[ {f\left( x \right)} \right]}^2}}}\) với mọi \(x \in \left( {0; + \infty } \right)\). Giá trị \(f\left( 3 \right)\) bằng

(THPT Kim Liên – Hà Nội – 2022) Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( x \right) > 0,\forall x > \frac{1}{2}\) và có đạo hàm \(f’\left( x \right)\) liên tục trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\) thỏa mãn \(f’\left( x \right) + 8x{f^2}\left( x \right) = 0,\forall x > \frac{1}{2}\) và \(f\left( 1 \right) = \frac{1}{3}\). Tính \(f\left( 1 \right) + f\left( 2 \right) + \;…\; + f\left( {1011} \right)\).

(THPT Kinh Môn – Hải Dương – 2022) Cho \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\,\left( {a \ne 0} \right)\) là hàm số nhận giá trị không âm trên đoạn \(\left[ {2;\,3} \right]\) có đồ thị \(y = f’\left( x \right)\) như hình vẽ

Biết diện tích hình giới hạn bởi các đồ thị của các hàm \(g\left( x \right) = x{f^2}\left( x \right)\,;\,\,\,h\left( x \right) = – {x^2}f\left( x \right)f’\left( x \right)\) và các đường \(x = 2;x = 3\) bằng 72. Tính \(f\left( 1 \right)\) ?

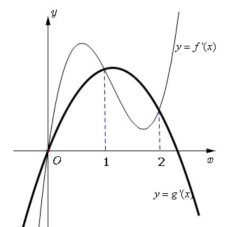
(THPT Phù Cừ – Hưng Yên – 2022) Cho hai hàm số \(f(x)\) và \(g(x)\) liên tục trên \(\mathbb{R}\) và hàm số \(f\prime (x) = a{x^3} + b{x^2} + cx + d\), \(g\prime (x) = q{x^2} + nx + p\) với \(a,q \ne 0\) có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f\prime (x)\) và \(y = g\prime (x)\) bằng \(\frac{5}{2}\) và \(f(2) = g(2)\). Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f(x)\) và \(y = g(x)\) bằng \(\frac{a}{b}\) (với \(a,b \in \mathbb{N}\) và \(a,b\) nguyên tố cùng nhau). Tính \(T = {a^2} – {b^2}\).

(THPT Võ Nguyên Giáp – Quảng Bình – 2022) Cho hàm số \(y = f\left( x \right)\) liên tục và nhận giá trị không âm trên \(\left[ { – 1;2} \right]\) và thoả mãn \(f\left( x \right) = f\left( {1 – x} \right),\;\forall x \in \left[ { – 1;2} \right]\). Đặt \({S_1} = \int\limits_{ – 1}^2 {xf\left( x \right){\rm{d}}x} \), \({S_2}\)là diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = – 1;\;x = 2\). Khẳng định nào dưới đây là đúng?

(Sở Phú Thọ 2022) Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3{x^2}\ln \left( {x + 1} \right) & {\rm{khi}}\,\,x \ge 0\\2x\sqrt {{x^2} + 3} + 1 & {\rm{khi}}\,\,x < 0\end{array} \right.\). Biết \(\int\limits_{\frac{1}{e}}^e {\frac{{f\left( {\ln x} \right)}}{x}{\rm{d}}x} = a\sqrt 3 + b\ln 2 + c\) với \(a,b,c \in \mathbb{Q}\). Giá trị của \(a + b + 6c\) bằng