Câu hỏi:
Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Lời Giải:
Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG
A. \(\frac{1}{{\sqrt[3]{2}}}\).
B. \(\frac{3}{{1 + 2\sqrt 2 … [Đọc thêm...] vềMột miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Trắc nghiệm Ứng dụng Tích phân
Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Cho hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt tại \(A,B\) phân biệt sao cho \(OB = 2OA\).
Câu hỏi: Cho hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt … [Đọc thêm...] vềCho hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt tại \(A,B\) phân biệt sao cho \(OB = 2OA\).
Cho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f’\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( – 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { – b – c\,;\,d} \right)\). Tính diện tích hình phẳng giới hạn bởi đường thẳng \(\Delta \) và đồ thi hàm số \(f\left( x \right)\) được tính bởi công thức
Câu hỏi: Cho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f'\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( - 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { - b - c\,;\,d} \right)\). Tính diện tích hình phẳng giới … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f’\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( – 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { – b – c\,;\,d} \right)\). Tính diện tích hình phẳng giới hạn bởi đường thẳng \(\Delta \) và đồ thi hàm số \(f\left( x \right)\) được tính bởi công thức
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 3\); \( - 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
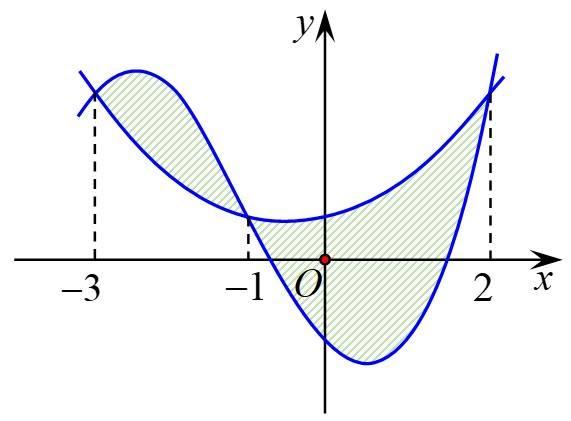
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( – 3; – 1;2\) .
Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( - 3; - 1;2\) .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( – 3; – 1;2\) .
Cho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = – 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị nằm trong khoảng nào sau đây?
Câu hỏi: Cho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( - 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = - 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = … [Đọc thêm...] vềCho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = – 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị nằm trong khoảng nào sau đây?
69. Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là
Câu hỏi: 69. Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là A. \(\frac{\pi }{2}\left( {{e^2} - 1} \right)\). B. \(\pi \left( {{e^2} + 1} \right)\). C. \(\frac{\pi }{2}\left( {{e^2} + 1} … [Đọc thêm...] về69. Gọi \(\left( H \right)\)là hình phẳng giới hạn bởi đồ thị hàm số \(y = {e^x}\), trục \(Ox\)và hai đường thẳng \(x = 0,\) \(x = 1\). Thể tích của khối tròn xoay tạo thành khi quay \(\left( H \right)\) xung quanh trục\(Ox\) là
98. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f’\left( x \right)\) như hình bên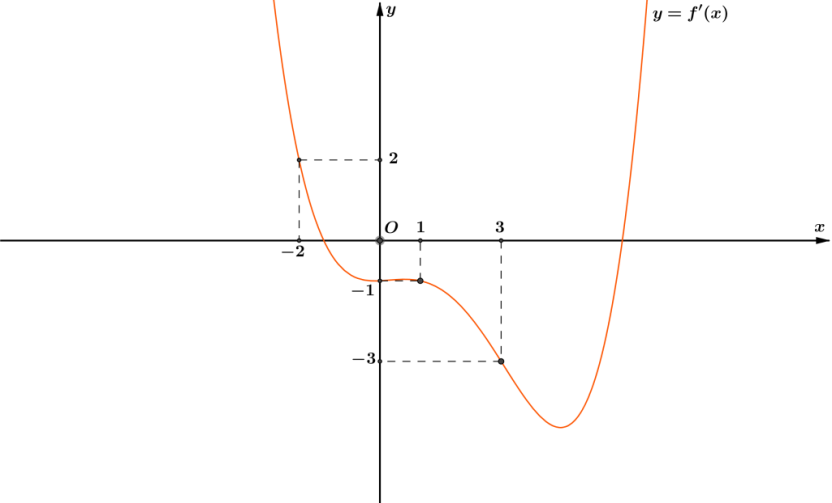
Xét hàm số \(g\left( x \right) = 2f\left( x \right) + {x^2}\). Hỏi mệnh đề nào sau đây là đúng?
Câu hỏi: 98. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f'\left( x \right)\) như hình bên Xét hàm số \(g\left( x \right) = 2f\left( x \right) + {x^2}\). Hỏi mệnh đề nào sau đây là đúng? A. \(g\left( 1 \right) < g\left( { - 2} \right) < g\left( 3 \right)\). B. \(g\left( { - 2} \right) > g\left( 3 \right) = … [Đọc thêm...] về98. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị hàm số \(y = f’\left( x \right)\) như hình bên
Xét hàm số \(g\left( x \right) = 2f\left( x \right) + {x^2}\). Hỏi mệnh đề nào sau đây là đúng?
88. Một viên gạch hoa hình vuông cạnh\(40\,cm\) được thiết kế như hình bên dưới. Diện tích mỗi cánh hoa bằng
Câu hỏi: 88. Một viên gạch hoa hình vuông cạnh\(40\,cm\) được thiết kế như hình bên dưới. Diện tích mỗi cánh hoa bằng A. \(\frac{{800}}{3}c{m^2}\). B. \(\frac{{400}}{3}\,c{m^2}\). C. \(250\,c{m^2}\). D. \(800\,c{m^2}\). Lời giải Diện tích một cánh hoa là diện tích hình phẳng được tính theo công thức sau: \(S = \int\limits_0^{20} {\left( {\sqrt … [Đọc thêm...] về88. Một viên gạch hoa hình vuông cạnh\(40\,cm\) được thiết kế như hình bên dưới. Diện tích mỗi cánh hoa bằng
89. Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước . Tính thể tích mà chiếc lu chứa được. 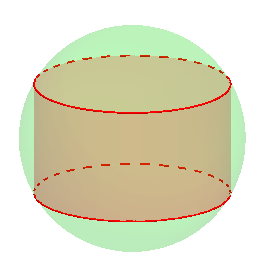
Câu hỏi: 89. Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước . Tính thể tích mà chiếc lu chứa được. A. \(\frac{{100}}{3}\pi \left( {d{m^3}} \right)\). B. \(\frac{{43}}{3}\pi \left( … [Đọc thêm...] về89. Một khối cầu có bán kính là \(5\left( {dm} \right)\), người ta cắt bỏ hai phần của khối cầu bằng hai mặt phẳng song song cùng vuông góc đường kính và cách tâm một khoảng \(3\left( {dm} \right)\) để làm một chiếc lu đựng nước . Tính thể tích mà chiếc lu chứa được.
