Câu hỏi: Cho hàm số \(f\left( x \right) = {e^{{x^2} - 2x}}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) thoả mãn điều kiện hàm số \(g\left( x \right) = \left| {f\left( {\left| {2m - x} \right| + 2} \right) - 1} \right|\) đồng biến trên khoảng \(\left( {2020\,;\, + \infty } \right)\)? A. 1010. B. 2020. C. 1011. D. 2019. LỜI GIẢI CHI TIẾT Ta có: … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {e^{{x^2} – 2x}}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) thoả mãn điều kiện hàm số \(g\left( x \right) = \left| {f\left( {\left| {2m – x} \right| + 2} \right) – 1} \right|\) đồng biến trên khoảng \(\left( {2020\,;\, + \infty } \right)\)?
Trắc nghiệm Tính đơn điệu của hàm số
Cho hàm số \(y = f\left( x \right)\) có đồ thị nằm trên trục hoành và có đạo hàm trên \(\mathbb{R}\), bảng xét dấu biểu thức \(f’\left( x \right)\) như bảng dưới đây

Hàm số \(y = g\left( x \right) = \frac{{f\left( {{x^2} – 2x} \right)}}{{f\left( {{x^2} – 2x} \right) + 1}}\) nghịch biến trên khoảng nào dưới đây?
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đồ thị nằm trên trục hoành và có đạo hàm trên \(\mathbb{R}\), bảng xét dấu biểu thức \(f'\left( x \right)\) như bảng dưới đây Hàm số \(y = g\left( x \right) = \frac{{f\left( {{x^2} - 2x} \right)}}{{f\left( {{x^2} - 2x} \right) + 1}}\) nghịch biến trên khoảng nào dưới đây? A. \(\left( { - \infty \,;\,1} \right)\). B. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đồ thị nằm trên trục hoành và có đạo hàm trên \(\mathbb{R}\), bảng xét dấu biểu thức \(f’\left( x \right)\) như bảng dưới đây
Hàm số \(y = g\left( x \right) = \frac{{f\left( {{x^2} – 2x} \right)}}{{f\left( {{x^2} – 2x} \right) + 1}}\) nghịch biến trên khoảng nào dưới đây?
Cho hàm số \(f\left( x \right) = \frac{1}{4}{x^4} – {x^3} + 2x – 1\). Đặt \(g\left( x \right) = f\left( {x – \frac{m}{3}} \right) – \frac{1}{2}{\left( {x – \frac{m}{3} – 1} \right)^2} + m + 1\), với \(m\) là tham số. Gọi \(S\) là tập hợp tất cả các số nguyên dương \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {7\,;\,8} \right)\). Tổng các phần tử có trong tập \(S\) bằng
Câu hỏi: Cho hàm số \(f\left( x \right) = \frac{1}{4}{x^4} - {x^3} + 2x - 1\). Đặt \(g\left( x \right) = f\left( {x - \frac{m}{3}} \right) - \frac{1}{2}{\left( {x - \frac{m}{3} - 1} \right)^2} + m + 1\), với \(m\) là tham số. Gọi \(S\) là tập hợp tất cả các số nguyên dương \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {7\,;\,8} \right)\). Tổng các … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = \frac{1}{4}{x^4} – {x^3} + 2x – 1\). Đặt \(g\left( x \right) = f\left( {x – \frac{m}{3}} \right) – \frac{1}{2}{\left( {x – \frac{m}{3} – 1} \right)^2} + m + 1\), với \(m\) là tham số. Gọi \(S\) là tập hợp tất cả các số nguyên dương \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {7\,;\,8} \right)\). Tổng các phần tử có trong tập \(S\) bằng
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ sau:

giá trị của \(a\) để hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2} – a} \right|\) đồng biến trên khoảng \(\left( { – 2\,;\,0} \right)\) và nghịch biến trên khoảng \(\left( {0\,;\,4} \right)\) là
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ sau: giá trị của \(a\) để hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2} - a} \right|\) đồng biến trên khoảng \(\left( { - 2\,;\,0} \right)\) và nghịch biến trên khoảng \(\left( {0\,;\,4} \right)\) là A. \(a \le 4f\left( { - 2} \right) + 4\). B. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f’\left( x \right)\) như hình vẽ sau:
giá trị của \(a\) để hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2} – a} \right|\) đồng biến trên khoảng \(\left( { – 2\,;\,0} \right)\) và nghịch biến trên khoảng \(\left( {0\,;\,4} \right)\) là
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ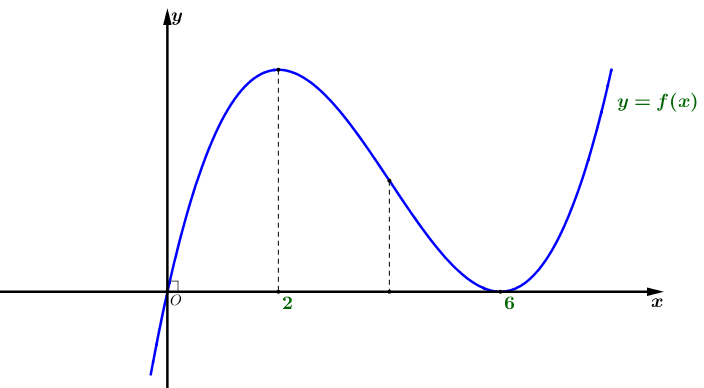
Đặt \(g\left( x \right) = \frac{1}{{f\left( {2\sqrt x + \sqrt {6 – 2x} + m} \right)}}\). Có bao biêu giá trị \(m\) nguyên để hàm số \(g\left( x \right)\) nghịch biến trên \(\left( {2\,;\,3} \right)\)?
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ Đặt \(g\left( x \right) = \frac{1}{{f\left( {2\sqrt x + \sqrt {6 - 2x} + m} \right)}}\). Có bao biêu giá trị \(m\) nguyên để hàm số \(g\left( x \right)\) nghịch biến trên \(\left( {2\,;\,3} \right)\)? A. \(4.\) B. \(2.\) C. 3. D. \(1.\) LỜI GIẢI CHI TIẾT + Đặt \(t = 2\sqrt x + \sqrt … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ
Đặt \(g\left( x \right) = \frac{1}{{f\left( {2\sqrt x + \sqrt {6 – 2x} + m} \right)}}\). Có bao biêu giá trị \(m\) nguyên để hàm số \(g\left( x \right)\) nghịch biến trên \(\left( {2\,;\,3} \right)\)?
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Biết hàm số \(f’\left( x \right)\) có đồ thị như hình vẽ, có bao nhiêu giá trị nguyên của \(m\) thuộc \(\left[ { – 2019;2019} \right]\) để hàm số \(g\left( x \right) = f\left( {{{2019}^x}} \right) – mx + 2\) đồng biến trên \(\left[ {0;1} \right]\)?

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Biết hàm số \(f'\left( x \right)\) có đồ thị như hình vẽ, có bao nhiêu giá trị nguyên của \(m\) thuộc \(\left[ { - 2019;2019} \right]\) để hàm số \(g\left( x \right) = f\left( {{{2019}^x}} \right) - mx + 2\) đồng biến trên \(\left[ {0;1} \right]\)? A. 2018. B. 2019. C. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}\). Biết hàm số \(f’\left( x \right)\) có đồ thị như hình vẽ, có bao nhiêu giá trị nguyên của \(m\) thuộc \(\left[ { – 2019;2019} \right]\) để hàm số \(g\left( x \right) = f\left( {{{2019}^x}} \right) – mx + 2\) đồng biến trên \(\left[ {0;1} \right]\)?
Cho hàm số \(y = f\left( x \right) = \left| { – \frac{1}{3}{x^3} + \frac{1}{2}\left( {2m + 3} \right){x^2} – \left( {{m^2} + 3m} \right)x + \frac{2}{3}} \right|\). Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 9\,;\,9} \right]\) để hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( {1\,;\,2} \right)\)?
Câu hỏi: Cho hàm số \(y = f\left( x \right) = \left| { - \frac{1}{3}{x^3} + \frac{1}{2}\left( {2m + 3} \right){x^2} - \left( {{m^2} + 3m} \right)x + \frac{2}{3}} \right|\). Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 9\,;\,9} \right]\) để hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( {1\,;\,2} \right)\)? A. \(3\). B. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = \left| { – \frac{1}{3}{x^3} + \frac{1}{2}\left( {2m + 3} \right){x^2} – \left( {{m^2} + 3m} \right)x + \frac{2}{3}} \right|\). Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 9\,;\,9} \right]\) để hàm số \(y = f\left( x \right)\) nghịch biến trên khoảng \(\left( {1\,;\,2} \right)\)?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( { – 2} \right) = 10\), \(f\left( 4 \right) = 1000\). Biết \(y = f’\left( x \right)\) có đồ thị như hình vẽ dưới đây.
Hàm số \(y = g\left( x \right) = {f^2}\left( x \right) – 2020f\left( x \right)\) đồng biến trên những khoảng nào dưới đây?
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( { - 2} \right) = 10\), \(f\left( 4 \right) = 1000\). Biết \(y = f'\left( x \right)\) có đồ thị như hình vẽ dưới đây. Hàm số \(y = g\left( x \right) = {f^2}\left( x \right) - 2020f\left( x \right)\) đồng biến trên những khoảng nào dưới đây? A. \(\left( { - 2\,;1} \right)\) … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thoả mãn \(f\left( { – 2} \right) = 10\), \(f\left( 4 \right) = 1000\). Biết \(y = f’\left( x \right)\) có đồ thị như hình vẽ dưới đây.
Hàm số \(y = g\left( x \right) = {f^2}\left( x \right) – 2020f\left( x \right)\) đồng biến trên những khoảng nào dưới đây?
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Hàm số \(f’\left( {3 – 2x} \right)\) có đồ thị như hình vẽ

Hỏi hàm số \(f\left( x \right)\) nghịch biến trên khoảng nào sau đây?
Câu hỏi: Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Hàm số \(f'\left( {3 - 2x} \right)\) có đồ thị như hình vẽ Hỏi hàm số \(f\left( x \right)\) nghịch biến trên khoảng nào sau đây? A. \(\left( { - \infty ; - 1} \right)\). B. \(\left( {0; + \infty } \right)\) C. \(\left( {3; + \infty } \right)\). D. \(\left( {0;2} \right)\). LỜI GIẢI … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Hàm số \(f’\left( {3 – 2x} \right)\) có đồ thị như hình vẽ
Hỏi hàm số \(f\left( x \right)\) nghịch biến trên khoảng nào sau đây?
Cho hàm số \(y = {\left( {\sqrt {{x^2} + 1} – x} \right)^3} – m\left( {2{x^2} – 2x\sqrt {{x^2} + 1} + 1} \right) – \frac{{m – 6}}{{\sqrt {{x^2} + 1} + x}} – 1\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\).
Câu hỏi: Cho hàm số \(y = {\left( {\sqrt {{x^2} + 1} - x} \right)^3} - m\left( {2{x^2} - 2x\sqrt {{x^2} + 1} + 1} \right) - \frac{{m - 6}}{{\sqrt {{x^2} + 1} + x}} - 1\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\). A. \(5\). B. Vô số. C. \(3\). D. Không tồn tại \(m\). LỜI GIẢI CHI TIẾT Hàm số \(y = {\left( … [Đọc thêm...] vềCho hàm số \(y = {\left( {\sqrt {{x^2} + 1} – x} \right)^3} – m\left( {2{x^2} – 2x\sqrt {{x^2} + 1} + 1} \right) – \frac{{m – 6}}{{\sqrt {{x^2} + 1} + x}} – 1\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số nghịch biến trên \(\mathbb{R}\).
