Câu hỏi:
Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Lời Giải:
Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG
A. \(\frac{1}{{\sqrt[3]{2}}}\).
B. \(\frac{3}{{1 + 2\sqrt 2 … [Đọc thêm...] vềMột miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
VDC Toan 2022
Một miếng đất dạng hình parabol chiều dài 18m, chiều rộng 12m. Người ta chia miếng đất bằng 2 đoạn thẳng song song \(AB,CD\) thành ba phần có diện tích bằng nhau . Tỉ số \(\frac{{AB}}{{C{\rm{D}}}}\) bằng:
Cho hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt tại \(A,B\) phân biệt sao cho \(OB = 2OA\).
Câu hỏi: Cho hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt … [Đọc thêm...] vềCho hàm số \(y = \frac{1}{3}{x^3} – 2{x^2} + 3x – 1\) có đồ thị \(\left( C \right)\). Gọi \(M,N\) là hai điểm thuộc \(\left( C \right)\) sao cho tiếp tuyến tại \(M,N\) song song với nhau. Khi đó diện tích hình phẳng giới hạn bởi \(\left( C \right)\) và đường thẳng \(MN\) nằm trong khoảng nào dưới đây? Biết rằng đường thẳng \(MN\) cắt trục hoành, trục tung lần lượt tại \(A,B\) phân biệt sao cho \(OB = 2OA\).
Cho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f’\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( – 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { – b – c\,;\,d} \right)\). Tính diện tích hình phẳng giới hạn bởi đường thẳng \(\Delta \) và đồ thi hàm số \(f\left( x \right)\) được tính bởi công thức
Câu hỏi: Cho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f'\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( - 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { - b - c\,;\,d} \right)\). Tính diện tích hình phẳng giới … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^3} + b{x^2} + cx + d\). Biết đồ thi hàm số \(f\left( x \right)\) có một điểm cực trị là \(A\) có hoành độ bằng \(1\), đồ thị \(y = f’\left( x \right)\) cắt trục tung tại điểm \(B\) có tung độ là \( – 5\). Gọi \(\Delta \) là đường thẳng đi qua hai điểm \(A\) và \(E\left( { – b – c\,;\,d} \right)\). Tính diện tích hình phẳng giới hạn bởi đường thẳng \(\Delta \) và đồ thi hàm số \(f\left( x \right)\) được tính bởi công thức
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng

Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( - 3\); \( - 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – \frac{1}{2}\) và \(g\left( x \right) = d{x^2} + ex + 1\), \(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt là \( – 3\); \( – 1\); \(1\) . Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
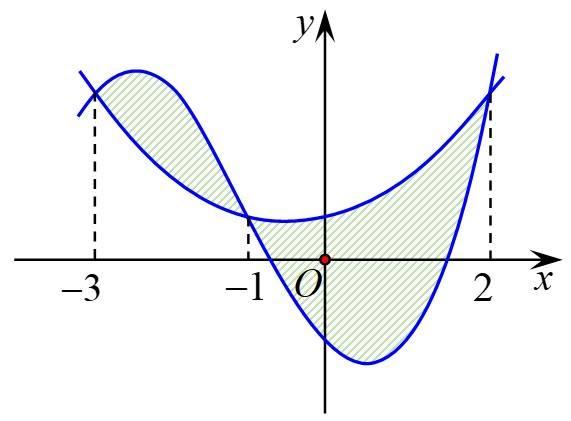
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( – 3; – 1;2\) .
Câu hỏi:
Cho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx - 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( - 3; - 1;2\) .
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích … [Đọc thêm...] vềCho hai hàm số \(f\left( x \right) = a{x^3} + b{x^2} + cx – 1\) và \(g\left( x \right) = d{x^2} + ex + \frac{1}{2}\)\(\left( {a,b,c,d,e \in \mathbb{R}} \right)\). Biết rằng đồ thị của hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) cắt nhau tại ba điểm có hoành độ lần lượt \( – 3; – 1;2\) .
Cho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = – 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị nằm trong khoảng nào sau đây?
Câu hỏi: Cho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( - 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = - 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = … [Đọc thêm...] vềCho hàm số \(y = f(x) = {x^3} + a{x^2} + bx + c\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\) và \(1\). Gọi \(y = g(x) = m{x^2} + nx + p\,\,\,(m < 0)\) là hàm số bậc hai có cực trị tại \(x = – 1\)và có đồ thị điqua điểm có hoành độ\(x = 1\) của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạnbởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị nằm trong khoảng nào sau đây?
Từ \(A\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\), gọi \(\left( P \right)\) là mặt phẳng chứa các tiếp điểm, biết \(\left( P \right)\) luôn đi qua một đường thẳng \(d\) cố định. Phương trình đường thẳng \(d\) là:
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {\left( {y + 3} \right)^2} + {z^2} = 36\) và điểm \(A\) nằm trên đường thẳng \(\Delta \) có phương trình \(\left\{ \begin{array}{l}x = 1 - t\\y = 3\\z = 1 - t\end{array} \right.\) và nằm ngoài mặt cầu \(\left( S \right)\). Từ \(A\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\), gọi \(\left( P \right)\) là … [Đọc thêm...] vềTừ \(A\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\), gọi \(\left( P \right)\) là mặt phẳng chứa các tiếp điểm, biết \(\left( P \right)\) luôn đi qua một đường thẳng \(d\) cố định. Phương trình đường thẳng \(d\) là:
Trong không gian cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 – 3t\end{array} \right.\). Ba điểm \(A\), \(B\), \(C\) phân biệt cùng thuộc mặt cầu sao cho \(MA\), \(MB\), \(MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( {1;1;2} \right)\). Tổng \(T = x_0^2 + y_0^2 + z_0^2\) bằng
Trong không gian cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 - 3t\end{array} \right.\). Ba điểm \(A\), \(B\), \(C\) phân biệt cùng thuộc mặt cầu sao cho \(MA\), \(MB\), \(MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( … [Đọc thêm...] vềTrong không gian cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 – 3t\end{array} \right.\). Ba điểm \(A\), \(B\), \(C\) phân biệt cùng thuộc mặt cầu sao cho \(MA\), \(MB\), \(MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( {1;1;2} \right)\). Tổng \(T = x_0^2 + y_0^2 + z_0^2\) bằng
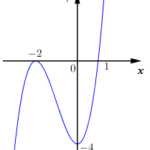
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( x \right) – \left( {m + 5} \right)\left| {f\left( x \right)} \right| + 4m + 4 = 0\) có 7 nghiệm phân biệt?
Cho hàm số \(y = f\left( x \right) = \,a\,{x^3} + b{x^2} + cx + d\) có đồ thị hàm số như hình bên dưới đây: Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( x \right) - \left( {m + 5} \right)\left| {f\left( x \right)} \right| + 4m + 4 = 0\) có 7 nghiệm phân biệt? A. \(1\) B. \(2\) C. \(3\) D. \(4\) Lời giải tham khảo: … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({f^2}\left( x \right) – \left( {m + 5} \right)\left| {f\left( x \right)} \right| + 4m + 4 = 0\) có 7 nghiệm phân biệt?
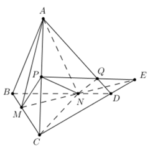
Cho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\)
Cho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\). Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) A. \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{26}}{{19}}\) … [Đọc thêm...] vềCho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\)