Câu hỏi:
(Sở Vĩnh Phúc 2022) Một người thợ cần thiết kế một bể cá hình hộp chữ nhật bằng kính, có chiều cao là \(0,8m\), thể tích \(576d{m^3}\). Biết rằng phần nắp phía trên của bể cá người thợ đó để trống một ô có diện tích bằng \(30\% \) diện tích đáy bể. Biết rằng loại kính mà người thợ sử dụng làm mặt bên và nắp bể có giá thành \(1000000\) đồng/m2 và kính để làm mặt … [Đọc thêm...] về (Sở Vĩnh Phúc 2022) Một người thợ cần thiết kế một bể cá hình hộp chữ nhật bằng kính, có chiều cao là \(0,8m\), thể tích \(576d{m^3}\). Biết rằng phần nắp phía trên của bể cá người thợ đó để trống một ô có diện tích bằng \(30\% \) diện tích đáy bể. Biết rằng loại kính mà người thợ sử dụng làm mặt bên và nắp bể có giá thành \(1000000\) đồng/m2 và kính để làm mặt đáy có giá thành \(1200000\) đồng/m2. Giả sử phần tiếp xúc giữa các mặt là không đáng kể. Số tiền mua kính ít nhất để hoàn thành bể cá gần nhất với số tiền nào dưới đây?
VDC Toan 2022
Cho hàm số \(y = f\left( x \right) = 6{x^4} + a{x^3} + b{x^2} + cx + d\quad \left( {a,b,c,d \in \mathbb{R}} \right)\). Biết đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị có hoành độ lần lượt là \( – 1;\;1;2\) và hàm số \(y = g\left( x \right)\)là hàm bậc hai có đồ thị đi ba điểm cực trị đó . Tính diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\); \(y = g\left( x \right)\)và trục \(Oy\).
Câu hỏi: Cho hàm số \(y = f\left( x \right) = 6{x^4} + a{x^3} + b{x^2} + cx + d\quad \left( {a,b,c,d \in \mathbb{R}} \right)\). Biết đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị có hoành độ lần lượt là \( - 1;\;1;2\) và hàm số \(y = g\left( x \right)\)là hàm bậc hai có đồ thị đi ba điểm cực trị đó . Tính diện tích hình phẳng giới hạn bởi các đường \(y = … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = 6{x^4} + a{x^3} + b{x^2} + cx + d\quad \left( {a,b,c,d \in \mathbb{R}} \right)\). Biết đồ thị hàm số \(y = f\left( x \right)\) có ba điểm cực trị có hoành độ lần lượt là \( – 1;\;1;2\) và hàm số \(y = g\left( x \right)\)là hàm bậc hai có đồ thị đi ba điểm cực trị đó . Tính diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\); \(y = g\left( x \right)\)và trục \(Oy\).
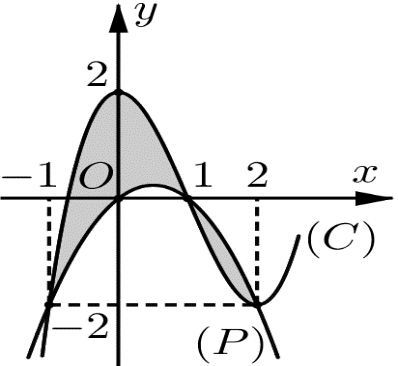
Hình phẳng được giới hạn bởi đồ thị \(\left( C \right)\) của hàm số đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Diện tích hình phẳng bằng
Câu hỏi:
Hình phẳng được giới hạn bởi đồ thị \(\left( C \right)\) của hàm số đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Diện tích hình phẳng bằng
Lời Giải:
Đây là các câu trắc nghiệm về ứng dụng tích phân mức độ 3,4 - VẬN DỤNG
A. \(\frac{5}{{12}}\).
B. \(\frac{7}{{12}}\).
C. \(\frac{{11}}{{12}}\).
D. … [Đọc thêm...] vềHình phẳng được giới hạn bởi đồ thị \(\left( C \right)\) của hàm số đa thức bậc ba và parabol \(\left( P \right)\) có trục đối xứng vuông góc với trục hoành. Diện tích hình phẳng bằng
Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có hai điểm cực tiểu \(\left( { – 1; – 2} \right);\left( {1; – 2} \right)\) và điểm cực đại \(\left( {0;3} \right)\). Hàm số\(y = g\left( x \right) = m{x^2} + nx + p\) có đồ thị đi qua các điểm cực trị của đồ thị \(y = f\left( x \right)\) . Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\)và\(y = g\left( x \right)\)gần bằng giá trị nào nhất trong các giá trị sau
Câu hỏi: Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có hai điểm cực tiểu \(\left( { - 1; - 2} \right);\left( {1; - 2} \right)\) và điểm cực đại \(\left( {0;3} \right)\). Hàm số\(y = g\left( x \right) = m{x^2} + nx + p\) có đồ thị đi qua các điểm cực trị của đồ thị \(y = f\left( x \right)\) . Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có hai điểm cực tiểu \(\left( { – 1; – 2} \right);\left( {1; – 2} \right)\) và điểm cực đại \(\left( {0;3} \right)\). Hàm số\(y = g\left( x \right) = m{x^2} + nx + p\) có đồ thị đi qua các điểm cực trị của đồ thị \(y = f\left( x \right)\) . Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\)và\(y = g\left( x \right)\)gần bằng giá trị nào nhất trong các giá trị sau
Cho hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + d\,\left( {a,b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị \( – 1\,,\,0\,,\,1\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng
Câu hỏi: Cho hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + d\,\left( {a,b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị \( - 1\,,\,0\,,\,1\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + d\,\left( {a,b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị \( – 1\,,\,0\,,\,1\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số \(y = f\left( x \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) bằng
Cho hàm số \(f\left( x \right) = – {x^3} + b{x^2} + cx + d{\rm{ }}\left( {b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\), \(\frac{5}{3}\) và có đồ thị cắt trục tung tại điểm có tung độ bằng \( – 2\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) và có đỉnh là \(I\left( {1;2} \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị thuộc khoảng nào sau đây
Câu hỏi: Cho hàm số \(f\left( x \right) = - {x^3} + b{x^2} + cx + d{\rm{ }}\left( {b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị là \( - 1\), \(\frac{5}{3}\) và có đồ thị cắt trục tung tại điểm có tung độ bằng \( - 2\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) và có đỉnh … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = – {x^3} + b{x^2} + cx + d{\rm{ }}\left( {b,c,d \in \mathbb{R}} \right)\) có hai điểm cực trị là \( – 1\), \(\frac{5}{3}\) và có đồ thị cắt trục tung tại điểm có tung độ bằng \( – 2\). Gọi \(y = g\left( x \right)\) là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số \(y = f\left( x \right)\) và có đỉnh là \(I\left( {1;2} \right)\). Diện tích hình phẳng giới hạn bởi hai đường \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có giá trị thuộc khoảng nào sau đây
Mặt sàn của một thang máy có dạng hình vuông \(ABCD\) cạnh \(2{\rm{m}}\) được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ trục tọa độ \(Oxy\) với \(O\) là tâm hình vuông sao cho \(A\left( {1;1} \right)\) như hình vẽ bên thì các đường cong \(OA\) có phương trình \(y = {x^2}\) và \(y = a{x^3} + bx\). Tính giá trị \(a.b\) biết rằng diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\) diện tích mặt sàn.

Câu hỏi:
Mặt sàn của một thang máy có dạng hình vuông \(ABCD\) cạnh \(2{\rm{m}}\) được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ trục tọa độ \(Oxy\) với \(O\) là tâm hình vuông sao cho \(A\left( {1;1} \right)\) như hình vẽ bên thì các đường cong \(OA\) có phương trình \(y = {x^2}\) và \(y = a{x^3} + bx\). Tính giá trị \(a.b\) … [Đọc thêm...] vềMặt sàn của một thang máy có dạng hình vuông \(ABCD\) cạnh \(2{\rm{m}}\) được lát gạch màu trắng và trang trí bởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ trục tọa độ \(Oxy\) với \(O\) là tâm hình vuông sao cho \(A\left( {1;1} \right)\) như hình vẽ bên thì các đường cong \(OA\) có phương trình \(y = {x^2}\) và \(y = a{x^3} + bx\). Tính giá trị \(a.b\) biết rằng diện tích trang trí màu sẫm chiếm \(\frac{1}{3}\) diện tích mặt sàn.
Cho hàm số \(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có \(f\left( 0 \right) = 1\) và ba điểm cực trị là \(0;1;2.\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng đi qua điểm \(A\left( {3;10} \right)\) có hệ số góc bằng 4 bằng
Câu hỏi: Cho hàm số \(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có \(f\left( 0 \right) = 1\) và ba điểm cực trị là \(0;1;2.\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng đi qua điểm \(A\left( {3;10} \right)\) có hệ số góc bằng 4 bằng Lời Giải: Đây là các câu trắc nghiệm về ứng … [Đọc thêm...] vềCho hàm số \(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) \(\left( {a,b,c,d \in \mathbb{R}} \right)\) có \(f\left( 0 \right) = 1\) và ba điểm cực trị là \(0;1;2.\) Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng đi qua điểm \(A\left( {3;10} \right)\) có hệ số góc bằng 4 bằng
Cho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( – \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = – 55\) .

Câu hỏi:
Cho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( - \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = - 55\) .
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?
Lời Giải:
Đây là các câu … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( – \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = – 55\) .
Cho hàm số \(y = f\left( x \right)\)là hàm đa thức bậc bốn và có đồ thị \((C)\) như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\,\)và \(y = f’\left( x \right)\)bằng \(\frac{{856}}{5}\). Tính diện tích hình phẳng giới hạn bởi đồ thị \((C)\) và parabol \((P)\) đi qua ba điểm cực trị của đồ thị \((C)\).

Câu hỏi:
Cho hàm số \(y = f\left( x \right)\)là hàm đa thức bậc bốn và có đồ thị \((C)\) như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\,\)và \(y = f'\left( x \right)\)bằng \(\frac{{856}}{5}\). Tính diện tích hình phẳng giới hạn bởi đồ thị \((C)\) và parabol \((P)\) đi qua ba điểm cực trị của đồ thị \((C)\).
Lời Giải: … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\)là hàm đa thức bậc bốn và có đồ thị \((C)\) như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y = f\left( x \right)\,\)và \(y = f’\left( x \right)\)bằng \(\frac{{856}}{5}\). Tính diện tích hình phẳng giới hạn bởi đồ thị \((C)\) và parabol \((P)\) đi qua ba điểm cực trị của đồ thị \((C)\).
