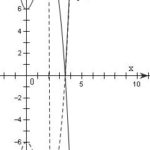
Đề bài: $1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x^3 - 3x^2 - 6$$2.$ Khi $a$ thay đổi hãy biện luận số nghiệm của phương trình: $| x^3 - 3x^2- 6| = a$ Lời giải $1.$ Bạn đọc tự giải$2.$ Trước hết dựng đồ thị y = $\left| {{x^3} - 3{x^2} - 6} \right|$Suy ra từ đồ thị vừa vẽ:Đường thẳng $y = a$ (song song với $Ox$) cắt đồ thị tại bao nhiêu điểm thì … [Đọc thêm...] vềĐề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x^3 – 3x^2 – 6$$2.$ Khi $a$ thay đổi hãy biện luận số nghiệm của phương trình: $| x^3 – 3x^2- 6| = a$
Ứng dụng hàm số vào giải toán
Đề: Cho $a,b,c$ là các hằng số thỏa mãn $\frac{a}{2010}+\frac{b}{2009}+\frac{c}{2008} = 0$. Chứng minh phương trình $ax^2 + bx + c=0$ có nghiệm trên $(0;1).$
Đề bài: Cho $a,b,c$ là các hằng số thỏa mãn $\frac{a}{2010}+\frac{b}{2009}+\frac{c}{2008} = 0$. Chứng minh phương trình $ax^2 + bx + c=0$ có nghiệm trên $(0;1).$ Lời giải Xét $f(x) = ax^{2009} + bx^{2008}+cx^{2007}, x \in R$$\Rightarrow F(x) = \int\limits_{0}^{x} f(t)dt = \frac{ax^{2010}}{2010} + \frac{bx^{2009}}{2009}+\frac{cx^{2008}}{2008}$ khả vi trên $R$ và thỏa mãn … [Đọc thêm...] vềĐề: Cho $a,b,c$ là các hằng số thỏa mãn $\frac{a}{2010}+\frac{b}{2009}+\frac{c}{2008} = 0$. Chứng minh phương trình $ax^2 + bx + c=0$ có nghiệm trên $(0;1).$
Đề: Chứng minh rằng phương trình : $ (4x-3) \log_{2010}x + \frac{2x^2-3x+1}{x\ln 2010} = 0$ có nghiệm trên $\left ( \frac{1}{2} ;1 \right )$
Đề bài: Chứng minh rằng phương trình : $ (4x-3) \log_{2010}x + \frac{2x^2-3x+1}{x\ln 2010} = 0$ có nghiệm trên $\left ( \frac{1}{2} ;1 \right )$ Lời giải Cần giải chi tiết … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình : $ (4x-3) \log_{2010}x + \frac{2x^2-3x+1}{x\ln 2010} = 0$ có nghiệm trên $\left ( \frac{1}{2} ;1 \right )$
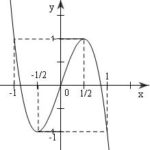
Đề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$
Đề bài: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x - 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 - 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$ Lời giải 1. Khảo sát , đồ thị (xin dành cho bạn đọc). Từ đồ thị hàm số: $y = 3x - 4{x^3}$ta suy ra đồ thị hàm số $y = |x|\left( {3 - 4{x^2}} … [Đọc thêm...] vềĐề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$
Đề: Cho $ m \in N.$ Tìm giá trị nhỏ nhất của: $f(x) = \int\limits_{1}^{x}t^m.e^{2t} -2 \left ( \frac{x^{m+3}}{m+3} +\frac{x^{m+2}}{m+2} \right ) , x\geq 1$
Đề bài: Cho $ m \in N.$ Tìm giá trị nhỏ nhất của: $f(x) = \int\limits_{1}^{x}t^m.e^{2t} -2 \left ( \frac{x^{m+3}}{m+3} +\frac{x^{m+2}}{m+2} \right ) , x\geq 1$ Lời giải Xét $ g(x) = e^{2x} - 2 (x^2 +x), x\geq 0$ $ g'(x) = 2e^{2x} - 2 (2x + 1) = 2 (e^{2x} -2x-1)$ $ g''(x) = 2 (2e^{2x} -2 ) = 4 (e^{2x}-1) \geq 0, \forall x \geq 0 $$\Rightarrow g' $ tăng trên … [Đọc thêm...] vềĐề: Cho $ m \in N.$ Tìm giá trị nhỏ nhất của: $f(x) = \int\limits_{1}^{x}t^m.e^{2t} -2 \left ( \frac{x^{m+3}}{m+3} +\frac{x^{m+2}}{m+2} \right ) , x\geq 1$
Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:$1/\,\,\,\,f(x) = \left| {{x^2} + 2x – 3} \right| + \frac{3}{2}\ln x$ trên đoạn $\left[ {\frac{1}{2},\,4} \right]$$2/\,\,\,\,\,f(x) = \left| {{x^2} + x – 2} \right| – \ln \frac{1}{x}$ trên đoạn $\left[ {\frac{1}{2},\,2} \right]$
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:$1/\,\,\,\,f(x) = \left| {{x^2} + 2x - 3} \right| + \frac{3}{2}\ln x$ trên đoạn $\left[ {\frac{1}{2},\,4} \right]$$2/\,\,\,\,\,f(x) = \left| {{x^2} + x - 2} \right| - \ln \frac{1}{x}$ trên đoạn $\left[ {\frac{1}{2},\,2} \right]$ Lời giải $1/$ Hàm số xác định trên đoạn $\left[ … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số:$1/\,\,\,\,f(x) = \left| {{x^2} + 2x – 3} \right| + \frac{3}{2}\ln x$ trên đoạn $\left[ {\frac{1}{2},\,4} \right]$$2/\,\,\,\,\,f(x) = \left| {{x^2} + x – 2} \right| – \ln \frac{1}{x}$ trên đoạn $\left[ {\frac{1}{2},\,2} \right]$
Đề: Giải hệ $\begin{cases}\frac{\tan x}{x}=\frac{\tan y}{y} \\ \sin x+\sin y=\sqrt{2} \end{cases} x,y \in (0;\frac{\pi}{2})$
Đề bài: Giải hệ $\begin{cases}\frac{\tan x}{x}=\frac{\tan y}{y} \\ \sin x+\sin y=\sqrt{2} \end{cases} x,y \in (0;\frac{\pi}{2})$ Lời giải Xét: $ f(t)=\frac{\tan t}{t}, t \in (0;\frac{\pi}{2})$ $ f'(t)=\frac{\frac{t}{\cos^2 t }-\tan t}{t^2}=\frac{2t-\sin 2t}{2t^2.\cos^2 t}>0, \forall t \in (0;\frac{\pi}{2})$ ( vì $|\sin u|0$) $\Rightarrow f (t)$ tăng trên … [Đọc thêm...] vềĐề: Giải hệ $\begin{cases}\frac{\tan x}{x}=\frac{\tan y}{y} \\ \sin x+\sin y=\sqrt{2} \end{cases} x,y \in (0;\frac{\pi}{2})$
Đề: $1$. Khảo sát hàm số \(y = – {x^4} + 5{x^2} – 4\)$2$. Xác định $m$ để phương trình \({x^4} – 5{x^2} – {m^2} + \sqrt 3 m = 0\) có $4$ nghiệm phân biệt
Đề bài: $1$. Khảo sát hàm số \(y = - {x^4} + 5{x^2} - 4\)$2$. Xác định $m$ để phương trình \({x^4} - 5{x^2} - {m^2} + \sqrt 3 m = 0\) có $4$ nghiệm phân biệt Lời giải $1$. Bạn đọc tự giải$2$. Đặt \(t = {x^2}\), phương trình đã cho trở thành \({t^2} - 5t - {m^2} + \sqrt 3 m = 0\left( 1 \right)\)Phương trình đã cho sẽ có 4 nghiệm phân biệt \( \Leftrightarrow \left( 1 … [Đọc thêm...] vềĐề: $1$. Khảo sát hàm số \(y = – {x^4} + 5{x^2} – 4\)$2$. Xác định $m$ để phương trình \({x^4} – 5{x^2} – {m^2} + \sqrt 3 m = 0\) có $4$ nghiệm phân biệt
Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$.
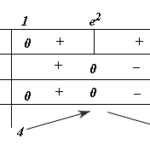
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$. Lời giải Ta có : $y'=\frac{2\ln x.\frac{1}{x}x - \ln^2x}{x^2}=\frac{\ln x(2-\ln x)}{x^2}$.Từ đó có bảng biến thiên sau:Vậy $\mathop {\max y }\limits_{ [1;e^3 ]}=y(e^2)=\frac{4}{e^2}\Leftrightarrow x=e^2$$\min y=\mathop {\min y }\limits_{ [1;e^3 ]}=\min (y(1);y(e^3))=\min … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$.
Đề: Cho hàm số: $y = x + 1 + \frac{1}{x – 1}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ đồ thị trên, hãy suy ra số nghiệm $x \in \left( {0 ; \frac{\pi }{2}} \right)$ của phương trình $1+\sin x+\cos x+\frac{1}{2}(\tan x + \cot x +\frac{1}{\sin x}+\frac{1}{\cos x})=m$tùy theo giá trị của tham số $m$
Đề bài: Cho hàm số: $y = x + 1 + \frac{1}{x - 1}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ đồ thị trên, hãy suy ra số nghiệm $x \in \left( {0 ; \frac{\pi }{2}} \right)$ của phương trình $1+\sin x+\cos x+\frac{1}{2}(\tan x + \cot x +\frac{1}{\sin x}+\frac{1}{\cos x})=m$tùy theo giá trị của tham số $m$ Lời giải $1)$ $y = x + 1 + \frac{1}{{x - 1}}$Hàm số xác … [Đọc thêm...] vềĐề: Cho hàm số: $y = x + 1 + \frac{1}{x – 1}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ đồ thị trên, hãy suy ra số nghiệm $x \in \left( {0 ; \frac{\pi }{2}} \right)$ của phương trình $1+\sin x+\cos x+\frac{1}{2}(\tan x + \cot x +\frac{1}{\sin x}+\frac{1}{\cos x})=m$tùy theo giá trị của tham số $m$